Del espíritu crítico y sus aplicaciones prácticas (y aéreas)
La historia que quiero contar acá empieza como tantas otras que usted ha leído pero la repetición no la hace menos angustiosa. Es que así como en el ajedrez las primeras jugadas son (o parecen) iguales a las de otras partidas, después, la variedad de posibilidades le va dibujando un nuevo destino. Créame que ésta lo tiene. Acompáñeme por acá..
Abraham Wald nació en 1902 en lo que en su momento fue Klausenburg, en el Imperio Austro-Húngaro. Sin embargo, al finalizar la Primera Guerra Mundial, Klausenburg ya no se llamaba más así sino que le pusieron Cluj, y como tantas otras ciudades de aquella época, ya no era ni austríaca ni húngara: era parte de Rumania.
Wald era judío, nieto de un rabino. Como en tantos otros casos, su afición por la matemática lo llevó a estudiar a Viena (que todavía sigue siendo austríaca). El problema se generó después: cuando Wald se doctoró, en 1931, no podía conseguir un puesto como profesor en Austria justamente por su condición de judío. Desesperado porque se le negaba la oportunidad de progresar (y de trabajar), fue rescatado por Oskar Morgenstern* que se lo llevó a Estados Unidos, primero a Chicago, a la Comisión Cowles para Investigaciones en Economía y después a Colorado Springs, para que trabajara en econometría. La aspiración de Wald era capacitarse, pero no quedarse a vivir en América del Norte: quería volver a su país. El problema fue que como los nazis arrasaban con todo, a Wald no le quedó otra alternativa que quedarse donde no quería.
Como producto de sus trabajos y sus méritos terminó recibiendo una oferta que no quiso (ni pudo) rechazar: una posición en la Universidad de Columbia, en New York. Ahora bien: ¿por qué toda esta historia? Téngame un poquito más de paciencia.
Wald empezó a distinguirse por su capacidad de análisis, su agudeza y creatividad. Seguramente esas cualidades fueron las que se requerían para formar parte de un grupo conocido con las siglas SRG en inglés: Statistical Research Group (Grupo de Investigaciones en Estadística). Lo invitaron a participar y aceptó también. Europa quedaba cada vez más lejos.
La guerra se daba en diferentes frentes y en distintos lugares del mundo más allá de los campos de batalla propiamente dichos. Mientras en el laboratorio de Los Alamos, a unos 150 kilómetros de Albuquerque, capital de New Mexico, se trabajaba en la fabricación de la bomba atómica en el famoso Proyecto Manhattan, en la Costa Este también había gran concentración de científicos teóricos, dedicados en particular a encontrar y resolver ecuaciones. Y vea lo que sucedió: tal era la potencia de lo que producía el grupo SRG que integraba Wald, que comenzaron a tener injerencia en lo que sucedía con los aviones que bombardeaban las posiciones nazis.
El grupo de matemáticos del SRG, especializados en estadística, comenzó a detectar que los militares contaban con ellos cada vez más. De hecho, el área militar recogía los datos y los trasladaba inmediatamente al departamento en donde operaba el grupo. El departamento estaba en un edificio ubicado exactamente a una cuadra de lo que hoy es la Universidad de Columbia (Columbia University), en el 401 oeste de la calle 118, en lo que se conoce hoy como el Upper West Manhattan.
Los militares esperaban las recomendaciones y sugerencias de los teóricos, los matemáticos. Por su parte, los ingenieros aeronáuticos convergían también al mismo departamento con la idea de analizar cómo implementar las modificaciones que sugirieran los matemáticos, siempre y cuando éstos pudieran mostrar que estos cambios podían mejorar la performance de las misiones aéreas.
La situación era (más o menos) así: cuando los bombarderos retornaban de sus misiones, no todos volvían intactos sino que al llegar a sus respectivas bases se hacía un análisis del impacto que habían producido los proyectiles alemanes. Se hacía un recuento de los diferentes lugares en donde se encontraban los ‘agujeros’. La idea era no sólo repararlos (obviamente), sino aprovechar la experiencia para proteger a los otros. A tal efecto, se buscaba agregarles armaduras o piezas metálicas que ofrecieran más resistencias a los impactos que recibían desde tierra.
Pero aparecía un problema: si uno le pone armaduras muy pesadas, el avión no puede volar; pierde maniobrabilidad y usa muchísimo más combustible. Por otro lado, si uno les pone armaduras muy livianas terminan resultando superfluas; es como si no existieran....¿para qué usarlas?
Aquí es donde empieza a intervenir la matemática (una vez más): ¿dónde está el punto de equilibrio, el punto óptimo? Ya que uno no puede proteger con armaduras todo el avión, entonces, ¿qué partes cuidar más? ¿Qué hacer?
Luego de que cada avión cumpliera con su misión, se hacía un reporte detallado de los distintos lugares (y el número) de los impactos que había recibido. Eso permitía elaborar un esquema como el que aparece en la Figura 1.

El diagrama muestra un ‘antes’ y un ‘después’. El avión de la derecha muestra que la mayoría del daño está hecho en los lugares más oscuros. Se advierte entonces que el avión había recibido las mayores averías en las alas, la nariz y el fuselaje, mientras que la cabina y la cola aparecían mucho más libre de los impactos.
Voy a agregar acá abajo una lista que reseña —en promedio— el número de impactos por ‘pie cuadrado’. ¿Qué es un ‘pie cuadrado’ y por qué no hago la conversión a centímetros cuadrados que nos es muchísimo más conocido? Un ‘pie’ mide un ‘poquito’ más que 30 centímetros. Por lo tanto, ‘un pie cuadrado’ imagínelo como una plancha de (30 x 30) centímetros cuadrados. Si usted se fija en la Figura 2, verá que si yo hiciera la conversión a centímetros cuadrados, aparecerían muchísimos decimales que terminarían distrayendo la atención de lo que me parece la idea central.
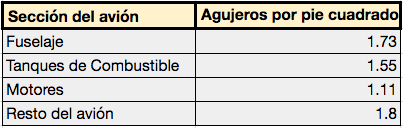
En definitiva, si uno focaliza su mirada en estos números, descubre que en el fuselaje se concentraba la mayoría de los disparos (casi dos agujeros por cada sector de (30x30) centímetros cuadrados), después en la zona de los tanques de nafta y por último los motores, que revelan el menor de los números en cuestión**.
En vista de estos resultados, los militares sugirieron que las áreas ‘grisadas’ fueran las que recibieran mayor protección: si se iban a incorporar más armaduras y placas metálicas, deberían distribuirse en esas zonas. ¡Error!
Sí, error. Wald hizo una explicación magistral: “Si los aviones regresan con daños en las zonas grisadas, es porque esas zonas son las que menos necesitan de las armaduras”. Después de todo, si los aviones podían recibir ese número de impactos pero podían regresar es porque allí no estaba el problema. Siguió Wald: “El hecho que la cabina y la cola tuvieran muchísimo menos impactos no tenía que ver con que los proyectiles no llegaban hasta ellas, sino que... (y aquí le pido que me preste atención)... los aviones que sufrían ese tipo de impactos, en esos lugares... ¡no retornaban más!”.
Aunque ahora parezca una trivialidad, la observación de Wald fue espectacular. Si había una distribución uniforme de los proyectiles, ¿dónde estaban los agujeros que faltaban? ¡Estaban en los aviones que faltaban, los aviones que no volvieron!”
Así de simple. Es que cabían dos alternativas: o bien los proyectiles que enviaban los nazis alcanzaban todas las partes del avión menos dos o bien los motores y las cabinas son los mayores puntos de vulnerabilidad. Había aviones que regresaban con agujeros en las alas, en el fuselaje, en la nariz pero muy pocos en los motores y en las cabinas. Y claro, eso sucedía porque los que impactaban allí... no volvían.
Ahora me lo imagino a usted pensando: ¿y dónde interviene la matemática en esta deducción, que ahora parece tan simple, sobre todo cuando ya conoce los hechos? Me lo imagino a usted también pensando: ‘Esa conclusión la hubiera podido sacar yo también’. Es posible, pero lo que subyace detrás de esta historia es la noción de que los aviones que regresaban constituían una muestra al azar de todos los aviones que salían... y como usted habrá detectado ya, ¡eso no era cierto!
Con el mismo tipo de razonamiento, en su libro How Not to Be Wrong (Cómo no estar equivocado), Jordan Ellenberg dice: “Si usted va a un hospital militar, en momentos en los que se está disputando una guerra, encontrará muchísimos más soldados con heridas/agujeros de bala en las piernas que en el pecho. Pero eso sucede no porque los combatientes no sufran balazos en el pecho sino porque los que reciben impactos allí no están en los hospitales: están muertos”
Las conclusiones de Wald iban exactamente en sentido contrario de las que podían aparecer como obvias. Y esto es particularmente crítico no solo en términos de ‘guerra y aviones, impactos de bala, proyectiles, etcétera’, sino que también tiene un particular uso en la vida cotidiana como se advierte en el uso que hoy le da la gente que conduce los destinos de Facebook. Sí, leyó bien: Facebook. Fíjese si no.
El director de investigaciones de Facebook, Nate Bolt, contó hace no mucho tiempo, cómo la historia de Wald lo impactó cuando aún era un estudiante en un laboratorio de la Universidad de California en San Diego. Como a usted no se le escapa, Facebook tiene una base de datos que posiblemente sea la más grande del mundo. La tentación de elaborar hipótesis sobre el comportamiento humano es enorme. Tener la posibilidad de ver cuáles son los gustos de la gente, en particular cuáles son sus gustos, mis gustos, inferir en función de ellos qué es lo que queremos, qué es lo que estaríamos dispuestos a comprar, a qué lugares querríamos viajar, qué inclinaciones tenemos por ciertos tipos de mujeres, de hombres, de marcas, de autos, libros, música, películas, obras de teatro, etcétera, etcétera.
Mirando lo que hacen las grandes mayorías invita, como decía más arriba, a sacar conclusiones que uno cree que están refrendadas por la abrumadora cantidad de datos disponibles. Sin embargo, eso no siempre es cierto. Bolt declaró: “Todos nosotros hemos producido, juntado y visto enormes cantidades de datos y los hemos analizado con múltiples de tipos de métricas, y es por eso que resulta tan fácil hacer inferencias equivocadas. Lo que yo creo es que hay una parte creativa en la comprensión de los datos cuantitativos que requieren una suerte de análisis artístico cuando uno investiga. En particular, y por poner un ejemplo, la investigación en diseño no se puede hacer como si fuera un laboratorio esterilizado para que no haya contaminaciones externas/humanas”.
La idea es mezclar la enorme cantidad de datos con casos individuales. “Es muy común que mirando los datos, cada uno de nosotros aparezca con conjeturas sobre ‘por qué la gente hace tal o cual cosa, procede de tal o cual manera o tiene tal tipo de comportamiento’, datos que uno juntó haciendo un análisis estadístico. Pero después, cuando uno mira las reacciones en la relación uno-a-uno, descubre que ¡no es así!”. Y sigue Bolt: “Es muy fácil quedarse empantanado en un lado o en el otro. Si uno pretende sacar conclusiones generales luego de analizar pequeños grupos puede producir un error difícil de detectar en función de la muestra que uno analiza. Por el otro lado, si uno se basa únicamente en el análisis de los grandes datos, termina perdiendo ‘el toque humano’”. Para Bolt, el ‘círculo constante’ de cuestionarse todas las hipótesis, termina siendo el gran desafío: lograr que las decisiones que toma la empresa den cuenta hasta del último ‘agujero de bala’, aún de aquellos que no se ven.
Como final: Wald y su mujer murieron el 13 de diciembre de 1950. Irónicamente, fueron dos de las víctimas cuando el avión en el que viajaban se estrelló en las montañas de Nilgiri, en el sur de la India. Hasta allí había ido invitado justamente por el gobierno indio, para dar conferencias sobre ‘Teoría de la Decisión’ y ‘Econometría’.
En definitiva, la historia de Abraham Wald pone una vez más en escena la creatividad humana, y la capacidad de análisis que pone en duda aún lo que parece obvio. De eso se trata el método científico, el espíritu crítico: dudar, dudar y dudar, no creer en las ‘autoridades académicas’, ni en ‘las verdades divinas o absolutas’.
Quiero terminar con esta frase (mía): “Venga y proponga su idea: discutámosla y convénzame con argumentos. No me grite y pretenda ganarme por la fuerza de su prepotencia. Explíqueme para que le entienda. En todo caso, dese usted también... la posibilidad de estar equivocado”.
--
*Economista alemán co-fundador junto a John Von Neumann (entre otras cosas) de lo que hoy se conoce como la Teoría de Juegos.
**Dejé para el final ‘resto del avión’, porque si bien aparece el número más grande es demasiado inespecífico y ambiguo.

Para suscribirte con $ 8.000/mes al Cohete hace click aquí
Para suscribirte con $ 10.000/mes al Cohete hace click aquí
Para suscribirte con $ 15.000/mes al Cohete hace click aquí
