Hace muchos años propuse un problema que salió publicado en Página 12[1] y también en uno de los libros de la saga “Matemática… ¿estás ahí?”. Pero ahora, después de 12 años quiero hacer un agregado y una variación. Espero poder generarle la misma sorpresa que me produjo a mí. El título que elegí es “¿Cómo aprendemos? Un doble desafío combinado”. Si sigue leyendo, entenderá por qué. Acá voy.
Voy a empezar por hacer un breve resumen de lo que escribí en el año 2007:
“¿Cuántas veces escuchó usted que los jóvenes “de hoy” leen un texto que no pueden comprender? O más aún: ¿cuántas veces fue usted quien pensó precisamente eso? Creo que queda claro que siempre es mucho más fácil descubrirlo o detectarlo en ‘los otros’ que verlo en uno mismo. Fíjese entonces qué es lo que le sugiere este problema de lógica. Me apuro en señalar que ¡no hace falta saber nada particular, sólo hay que querer pensar! Además, como no hay nadie alrededor suyo, ¿quién va a juzgar su respuesta?”
Aquí me detengo un instante, porque quiero hacer una reflexión:
¿No le parece mentira que yo tenga que escribir estas líneas para sugerirle que piense un problema? En fin… créame que vale la pena, y sobre todo para incrementar su propia autoestima. Verá que no me equivoco.
Sigo.
“Suponga que yo le muestro las siguientes cuatro cartas que aparecen apoyadas arriba de una mesa.
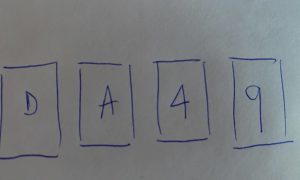
En principio, usted se sorprende porque habitualmente no conocemos ningún juego de cartas que presente esta peculiaridad, este tipo de naipes. Sin embargo, no se preocupe: son cartas que tienen, de un lado, una letra cualquiera del alfabeto español, y del otro lado, un número de un solo dígito, o sea, uno de estos diez números: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9.
Además, y esto es muy importante, yo le informo que las cartas cumplen con una regla que usted tendrá que comprobar:
“Si de un lado de una carta hay una vocal (a, e, i, o, u), del otro lado tiene que haber un número par (0, 2, 4, 6, 8).[2]
Ahora, mire las cuatro cartas que están arriba de la mesa: D, A, 4 y 9.
Yo le aseguro que alcanza con dar vuelta a lo sumo dos de las cuatro cartas para convencerse que la regla se cumple. En ese caso, ¿qué cartas daría vuelta usted, y por qué?
Llegado a este punto, voy a parar, porque quisiera dejarla/dejarlo para que usted pueda pensar cuáles cartas dar vuelta para estar convencido de que la regla se cumple. Tómese el tiempo que quiera, pero como respuesta, yo aspiro a que usted me diga: “Mirá: a lo sumo hay que dar vuelta estas dos cartas y con eso te va a alcanzar para decidir si se cumple la regla”.
Usted, ¿qué cartas daría vuelta?
Antes de avanzar, antes de seguir leyendo qué hice yo para contestar la pregunta, ¿no quiere pensar usted por su cuenta? ¿Qué gracia tendría que sea yo quien sugiera una (o ‘la’) solución?
------------------(aquí no se ve, pero se ha producido una pausa que usted está usando para pensar) --------------
Sigo. Estoy casi seguro que la primera carta (o una de las dos cartas) que usted decidió dar vuelta es la letra A. ¿Por qué? Es que si al dar vuelta la letra A (que es una vocal) no hubiera un número par, ¡listo! Es una situación directa: “doy vuelta la “A”; si no hay un número par se terminó la búsqueda. La regla estaría violada”. No haría falta dar vuelta ninguna otra carta.
Sigamos. Supongamos que sí, que había un número par detrás de la ‘A’. Todo bien, pero aún no sabemos si alguna de las otras tres cartas infringe la regla. De las tres cartas que quedan, podemos dar vuelta solamente una. ¿Cuál? ¿Usted qué piensa?
Analicemos -juntos- los tres casos que quedan:
- Empecemos con la letra ‘D’. ¿Aportará alguna información relevante lo que suceda del otro lado de la letra ‘D’? ¿Qué cree usted?
En verdad, si del otro lado de la ‘D’ hay un número par o un número impar, a los efectos de establecer lo que nos interesa, no ofrecerá nada nuevo, porque la regla no dice nada acerca de las letras que no sean vocales. Conclusión, podemos ignorar la letra ‘D’. No nos sirve.
- ¿Valdrá la pena dar vuelta la carta que tiene el número ‘4’? Aquí sí me quiero detener, y le propongo que piense por su cuenta sobre las dos posibilidades con las que nos podríamos encontrar:
Puede haber una vocal …. o no………………………………. (estos puntos suspensivos los escribí para darle tiempo a que piense).
Suponga que damos vuelta el ‘4’ y aparece una consonante. ¿Dice algo eso? ¿Nos aporta algo nuevo? Uno tiene la tentación de decir o esperar, que del otro lado del ‘4’ haya una vocal. Sin embargo, me gustaría que nos convenzamos juntos, que aunque eso suceda, no va a tener importancia. ¿Por qué? Es que la regla que queremos verificar, dice que
“detrás de cada vocal tiene que haber un número par”,
pero no dice que
“detrás de un número par “tiene que haber una vocal”.
¿Me entiende? Es muy importante que no avance sin haberme seguido en lo que estoy escribiendo. Es decir: vocal de un lado obliga a número par del otro. Pero, par de un lado, no obliga a nada.
En consecuencia, dar vuelta el número ‘4’ no nos va a aportar nada tampoco. Yo sé que la mayor tentación que tuvo usted (y créame que yo también), es en dar vuelta el ‘4’ para ver qué hay del otro lado, pero si me siguió en el razonamiento, verá que no hay ninguna necesidad de darla vuelta porque no va a decir nada nuevo, nada relevante para el problema que tenemos.
Conclusión: descartada la carta que tiene al ‘4’.
- Queda una última carta, la que exhibe al número ‘9’ (¿quiere pensar usted?).
Si la diéramos vuelta, ¿podríamos aprender algo que no sabíamos antes? Es decir, si al dar vuelta el 9 hubiera una vocal o una consonante, ¿altera lo que estamos tratando de comprobar? Es una buena oportunidad para que yo me tome otra pausa…..
Sigo: la respuesta es que sí. Si detrás del ‘9’ hubiera una consonante, no hay problema. En cambio, si detrás del número ‘9’ hubiera una vocal, entonces esto violentaría la regla porque ‘9’ no es un número par. Resulta relevante entonces, que al dar vuelta el número ‘9’ encontremos una consonante y no una vocal.
Y esto termina por resolver el problema original.
Lo que hay que hacer entonces, es -a lo sumo- dar vuelta la carta que tiene una ‘A’ de un lado y la carta que tiene un ‘9’. Lo que suceda del otro lado, determinará si la regla se cumple o no. Con la información que proveen estas dos cartas, podemos sacar la conclusión que buscamos. ¡y listo!
Esta primera parte fue la que escribí hace más de doce años. Sin embargo ahora, querría avanzar en otro sentido, y en el camino, hacernos (sí, hacernos, en primera persona del plural) algunas preguntas.
El matemático británico Keith Devlin[3] escribió en diciembre del año 2019 un artículo que sirvió (involuntariamente) de complemento de lo que yo había escrito hace tanto tiempo. Yo leí su artículo, y sirvió para educarme y al mismo tiempo, compartir con usted algunas preguntas. Creo que sería/será muy interesante entonces, que usted me acompañe en la lectura de lo que sigue y después vemos -juntos- si podemos extraer algunas conclusiones. Acá voy.
En principio, Devlin reproduce un experimento realizado por dos psicólogos norteamericanos en el año 1992, Leda Cosmides y John Tooby. Léalo con atención: es difícil de escribir (pero aproveche la Figura 2), pero muy sencillo de entender.
“Suponga que se realiza una cena en un salón que sirve para festejar el año nuevo. La concurrencia en su inmensa mayoría, está formada por gente joven, estudiantes de un colegio secundario y ligados también con una universidad local. Para poder consumir alcohol es necesario haber cumplido 21 años. Parte de su tarea esa noche, es verificar que no se viole esa regla: cualquier estudiante que no haya llegado a cumplir los 21 años, no podrá ingerir alcohol durante la cena. Para hacer todo más sencillo, digamos que en el bar solamente se podrá ordenar ‘cerveza’ o ‘gaseosa’. Y nada más.
Para facilitarle la tarea, todos los comensales, tienen que exhibir su DNI y dejarlo directamente apoyado arriba de la mesa en la que están cenando. Algunos lo exponen ‘hacia arriba’, de manera tal que con una simple ‘mirada’ usted podrá detectar la edad de su dueño/dueña, y otros, lo apoyaron ‘boca abajo’, de manera tal que si usted tuviera que verificar la edad de ese estudiante, no le quedará más remedio que ‘darlo vuelta’ para ver el año de nacimiento. Ah, y algo más: algunos vasos son de plástico, de manera que como son opacos, es imposible decidir desde ‘afuera’ si contienen cerveza o gaseosa.
Dicho todo esto, usted se acerca a una de las mesas en donde están comiendo cuatro personas y observa lo siguiente[4]: una está tomando una bebida gaseosa (persona 3) ya que tiene una copa de cristal en la mano y está a punto de beber y hay otra que también tiene una copa de vidrio transparente y usted puede determinar que el líquido es cerveza (persona 4). Señalo en principio estas dos porque ambas, como se ve en la Figura 2, tienen el documento de identidad ‘hacia abajo’ por lo que usted no puede decidir sin levantarlos y darlos vuelta, si son mayores de edad (o no). Puede decidir lo que están tomando, pero no sabe las edades.
Los otros dos estudiantes tienen el documento hacia arriba’y usted ve que uno (persona 2) es mayor de 21 años (por lo que puede tomar alcohol), mientras que la otra (persona 1) tiene 17 años (y no está en condiciones legales de consumir cerveza). Lamentablemente, ambos tienen sus vasos (de plástico) apoyados arriba de la mesa, y como son opacos usted no puede distinguir (desde afuera) si contienen cerveza o no. No le quedará más alternativa que levantarlos de la mesa y eventualmente, acercar su nariz para poder determinarlo con el olfato o verificar el contenido acercándoselo a sus ojos.
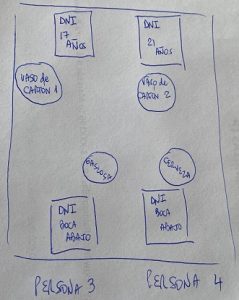
Ahora, tal como hice en el caso de las cartas, yo le aseguro que usted puede descubrir si los cuatro cumplen con la ley simplemente ‘oliendo’ o ‘mirando’ el contenido uno de los vasos y dando vuelta uno solo de los documentos. ¿Cuál documento y cuál bebida?
Ahora, otra vez, le toca a usted.
Antes de avanzar, usted advierte que los dos problemas parecen estar relacionados. Es decir, tanto el problema de las cartas que presenté más arriba, como este, parecen tener algunas similitudes. La idea es poder determinar si lo que aprendimos (usted y yo) en el caso anterior, sirve (o nos sirve) para deducir la solución de este segundo caso.
Sigo. Analicemos este caso particular, el de los mayores o menores de edad, consumiendo o no alcohol y después comparamos ambos casos.
Tomemos los dos estudiantes cuyas edades son visibles sin tocar el documento, o sea, las personas 1 y 2.
De los dos estudiantes que tienen el documento boca arriba, no le aportaría nada nuevo levantar el vaso de la persona 2 (ya que tiene 21 años): haya lo que haya en el vaso, está habilitado para consumir lo que quiera.
En cambio, en el caso de la persona 1 es distinto, porque como es menor de edad (usted ve que tiene 17 años), y por lo tanto, usted necesitará determinar el contenido del vaso. Ese es el vaso que usted tiene que oler o decidir visualmente si contiene cerveza (o no). Si contiene cerveza, estará violando la ley.
Ahora le propongo que sea usted quien decida qué hacer con las personas 3 y 4. Está claro que la persona 3 está tomando gaseosa y la persona 4 está tomando cerveza. Parece inmediato lo que hay que hacer:
Es lo único que falta determinar. Si es mayor de 21 años, está todo bien. Si no, está infringiendo la ley. Lo que suceda con la persona 3, es totalmente irrelevante.
¿Por qué hacer esta analogía? Estoy casi seguro que usted no tuvo ningún inconveniente para resolver el problema de la mayoría de edad y la bebida alcohólica (cerveza). Sin embargo, cuando pensamos el caso de las vocales y los números pares, eso ya fue otra historia. Si se detuvo a pensar, seguro que le llevó algún tiempo. Créame que lo mismo me pasa/pasó a mí (y Devlin afirma lo mismo en su artículo): a pesar de haber escrito sobre él y haber conocido de su existencia durante décadas, cada vez que me lo planteo, ¡necesito pensarlo otra vez! Y está muy bien que así sea, nadie dice que uno/yo tenga que recordar nada; lo que sí se me pide, es que piense, y si lo pude hacer alguna vez, ¿por qué no habría de poder tantas veces como me sea planteado?
Pero no quiero terminar sin hacer la comparación directa. Es decir, ¿cómo relacionar ambos problemas? ¿Cómo plantearlo de manera tal que la lógica que requiere resolver uno de ellos es exactamente equivalente o igual al otro?
La forma de conectarlos es la siguiente:
- Tomar alcohol (o cerveza en este caso) es equivalente a que haya una vocal
- Ser mayor de edad o haber cumplido 21 años, es equivalente a número par. Es decir, ser menor de edad es tener un número impar.
Mi propuesta final es la siguiente: plantéese ambos problemas nuevamente. Uno tendería a pensar que si pudo resolver el problema de las bebidas y la mayoría de edad primero, entonces estaría en mejores condiciones de resolver el de las cartas y los números pares. O al revés. Sin embargo (y en esto estoy simplemente reproduciendo lo que he leído), no parece que fuera el caso. La pregunta queda abierta (al menos para mí): ¿aprende uno o no? ¿encuentra las analogías o no? ¿Haber resuelto uno de los dos, hace más fácil la solución del segundo?
No tengo respuesta, no sé. Como siempre, uno tiene la tentación de sacar conclusiones generales o verdades absolutas, pero lamentablemente, la vida no ofrece muchas oportunidades de este tipo. Es por eso la fascinación que representa el estudio de la mente humana. Un verdadero desafío.
[1] https://www.pagina12.com.ar/diario/contratapa/13-92754-2007-10-10.html
[2] Sí, el número cero es un número par. Es motivo de otra nota, pero me apuro en decirle que ‘0’ es un múltiplo de ‘2’ (y por eso es par), ya que el número ‘0’ se puede escribir así: 0 = 2 x 0.
[3] Keith Devlin es un matemático británico que vive en Estados Unidos hace mucho tiempo. Es una de las personalidades más relevantes en el mundo en la difusión de la matemática así como en temas de educación. Devlin es hoy profesor en Stanford, en Palo Alto, California. Podría escribir mucho sobre él, pero le sugiero si le interesa que googlee su nombre, y se tropezará con una amplísima variedad de tópicos que ha cubierto con sus libros, artículos, ensayos. Sin ninguna duda, Devlin es hoy un referente mundial.
[4] Ver Figura 2
--------------------------------Para suscribirte con $ 8.000/mes al Cohete hace click aquí
Para suscribirte con $ 10.000/mes al Cohete hace click aquí
Para suscribirte con $ 15.000/mes al Cohete hace click aquí