Para sobrevivir, un buen soldado debe ante todo saber pensar
La historia que sigue es una versión adaptada de lo que –supuestamente— sucedió durante el siglo I. Sí, el siglo uno. Suena raro, ¿no? Más aún: esa historia dio origen a un problema clásico de la matemática/computación que sobrevivió el paso del tiempo. Se lo conoce con el nombre del “Problema de Josephus”, ya que se supone que fue Flavius Josephus [1], un historiador judío nacido en Jerusalén, quien describió la situación que vivieron él y 40 soldados que lo acompañaban.
En un momento determinado de la guerra judeo-romana, Josephus y su grupo cayeron en una emboscada y quedaron atrapados en una caverna rodeada de soldados enemigos. Después de debatir cómo proceder, optaron por suicidarse antes de ser capturados. Sin embargo, Josephus no estuvo de acuerdo con la propuesta y para que nadie tuviera que quitarse la vida, propuso el siguiente método:
“Sentémonos todos en un círculo. Alguno de nosotros empezará primero y matará a quien tenga sentado a la izquierda y así vamos a seguir hasta que –claramente— quedará nada más que uno solo de nosotros con vida. Ese será el único que tendrá que suicidarse”.
Fíjese en la Figura 1.
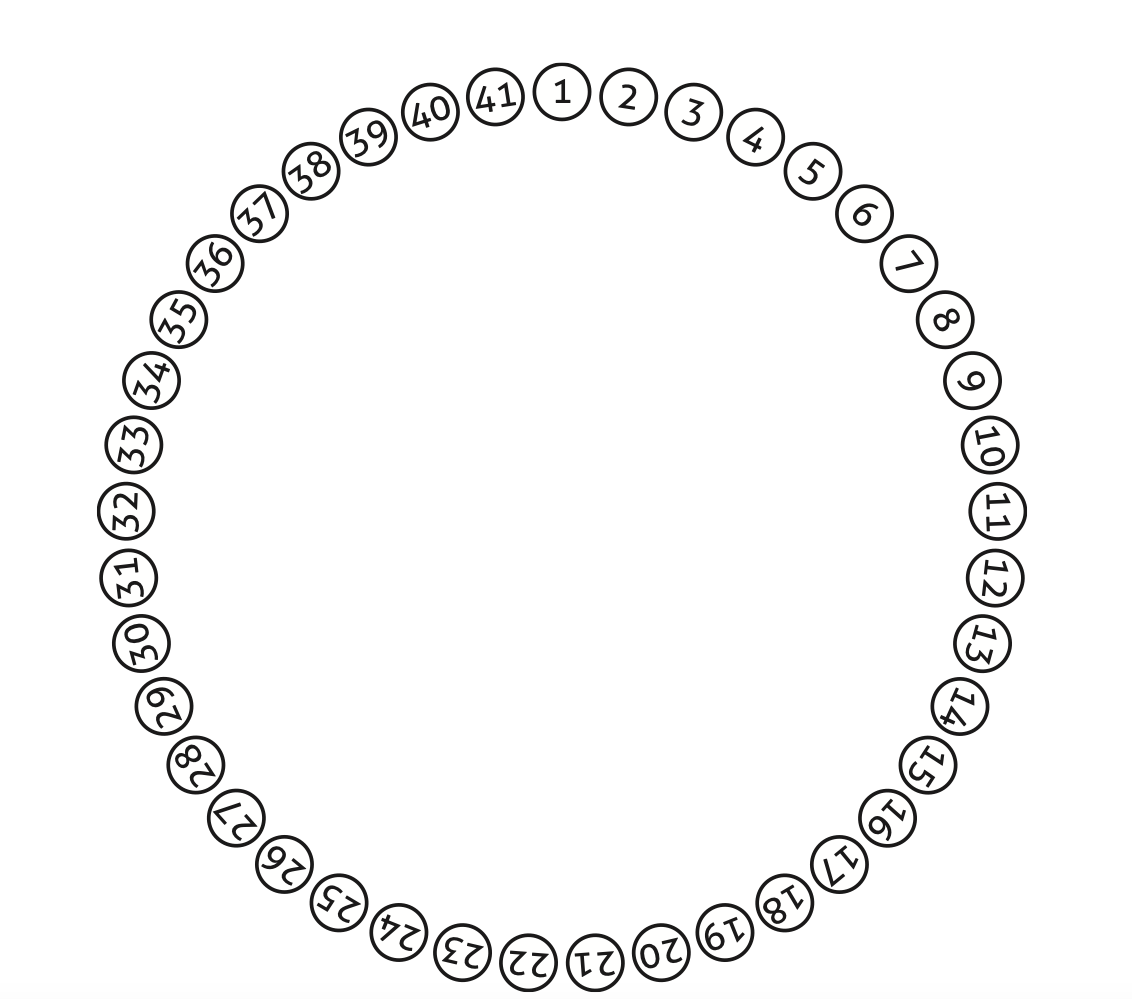
Allí están las cuarenta y un posiciones numeradas en forma creciente. Supongamos que empieza el que está sentado en la posición número 1. Ese soldado matará al 2. Luego, el 3 matará al 4, el 5 al 6... y así siguiendo. Como usted advierte, llegará un momento en el que habrán muerto todos los que están sentados en las posiciones que llevan un número par. Pero cuando muera el último de ellos, el número 40 (a manos del 39), el 41 estará vivo aún y ahora, el que tiene sentado a la izquierda es el número 1 quien había empezado con los asesinatos.
De acuerdo con las reglas, el 41 matará al 1, el 3 matará al 5, etc. Creo que ahora está claro que van a morir todos hasta que quede solamente uno con vida.
Es aquí donde aparece una parte interesante de la historia de Josephus. En principio, habrían de morir todos los soldados que estaban con Josephus en la caverna, pero la diferencia es que quien quedara último tendría que suicidarse... Más aún: el sobreviviente tendría que quitarse la vida y no habría ningún otro integrante del grupo que estuviera vivo para verificar que lo hiciera.
Como usted se imagina, Josephus eligió un lugar particular del círculo y se sentó allí. El sabía que siguiendo las reglas escritas más arriba, él habría de quedar como único sobreviviente. Esperó que todos estuvieran muertos, y en lugar de suicidarse, salió de la caverna y se entregó al enemigo.
Pregunta: ¿en qué lugar se sentó Josephus?
El problema es muy conocido en el mundo de la matemática y los programadores, y es por eso que hay muchísima literatura escrita sobre el tema, pero no hace falta saber nada particular para poder pensarlo. La versión que figura más arriba es solo una de las posibles variantes (la más sencilla) y si yo estuviera junto a usted, le sugeriría que no empiece con el caso de los 41 soldados, sino que intente con números más pequeños (de soldados) de manera tal de ver si le es posible intuir o imaginar una estrategia para determinar al ganador o sobreviviente a medida que va incrementando el número de soldados.
De la misma forma, una vez que hayamos resuelto el problema para 41 soldados, sería interesante pensar en una estrategia que permita deducir cuál será la posición ganadora en el caso general, es decir, independizarse del número 41 y encontrar alguna estrategia o fórmula que permita deducir el número que hay que elegir sin tener que recorrer todos los pasos intermedios.
Ideas para pensar la solución
Una solución posible, se sentarse con tiempo y empezar a recorrer el círculo con los 41 números ubicados como se ve en la Figura 1. Después de un rato, estoy seguro que usted encontrará la respuesta. Y no está mal resolver el problema de esta forma. De hecho, ¡encuentra la solución! ¿No era eso lo que quería? Sí, es verdad... es lo que quería, pero lo que sería interesante es ver si uno puede deducir otro tipo de respuesta. ¿A qué me refiero?
Es que por un lado es muy tedioso tener que recorrer todos los pasos intermedios. ¿No habrá otra forma de encontrar al ‘sobreviviente’?
Y por otro lado, ¿no le surge algún tipo de curiosidad que permita encontrar la respuesta para cualquier número de soldados? ¿Será posible encontrar una tal fórmula?
En fin: yo creo que sí, que vale la pena pensar en esas dos direcciones que apunté más arriba. Veamos si lo logro y en el camino la o lo seduzco a usted también. Acompáñeme por aquí.
Como propuse más arriba, empecemos con números más pequeños.
Si hubiera nada más que un solo soldado, no hay nada que pensar. El sobreviviente es el único participante (o soldado) que hay, y lo declaramos ganador.
En cambio, si hubiera dos soldados, entonces, el uno elimina al dos y allí se termina el juego también. Ganador: el número uno.
Sigo. Si ahora fueran tres soldados: 1-2-3.
En este caso, el 1 elimina al 2 pero el 3 está vivo aún y siguiendo el orden del círculo, el 3 elimina al 1. Ganador: número 3
Si fueran cuatro soldados: 1-2-3-4
Entonces 1 elimina a 2, y 3 elimina a 4. Quedan 1 y 3. El turno es otra vez para el número 1 que elimina al 3 y queda como único sobreviviente. Ganador: número 1.
Si fueran cinco soldados: 1-2-3-4-5
Voy un poco más rápido ahora. Quedan eliminados los dos pares (2 y 4), pero fíjese que ni bien queda eliminado el 4, el turno le corresponde al 5. O sea: sobreviven 5-1-3, pero 5 es el que empieza. Luego, 5 elimina al 1 y le toca el turno al 3. El 3 elimina al 5, y queda como sobreviviente. Ganador: número 3.
Una breve pausa. Ahora que advirtió lo que estoy haciendo, ¿no tiene ganas de seguir usted por su cuenta? Yo voy a seguir igual, pero... decía....
Si fueran seis soldados: 1-2-3-4-5-6
En el primer paso –como siempre— quedan eliminados todos los pares. Sobreviven 1-3-5. Después que 5 eliminó a 6, le toca una vez más al número 1.
El 1 elimina al 3.. y por último, el 5 elimina al 3. Ganador: número 5.
Para siete soldados: 1-2-3-4-5-6-7
En el primer paso quedan eliminados todos los pares, pero cuando queda afuera el número 6 (que es el último par), le toca el turno al número 7. Los que quedan son: 7-1-3-5, en ese orden.
El 7 elimina al 1, el 3 al 5, y quedan: 7 y 3, y es el turno del 7, que elimina al 3. Ganador: número 7.
Ahora voy a escribir una lista de los resultados que se obtienen al aumentar el número de personas que participan y le sugiero que la revise para verificar que los cálculos que hice son correctos.
Tabla 1
Número de personas Sobreviviente (o ganador)
1 1
2 1
3 3
4 1
5 3
6 5
7 7
8 1
9 3
10 5
11 7
12 9
13 11
14 13
15 15
16 1
17 3
18 5
19 7
20 9
21 11
22 13
23 15
24 17
25 19
26 21
27 23
28 25
29 27
30 29
31 31
32 1
33 3....
Antes de avanzar le pido que mire la lista con cuidado. ¿Qué ideas se le ocurren? ¿No se siente tentada/o de sacar algunas conclusiones?
Le sugiero que intente conjeturar una regla general para cualquier número de personas, aunque después tenga que modificarla... pero si sospecha alguna, escríbala en un papel y trate de verificar si usando los números que figuran más arriba, los resultados que usted obtiene son los que figuran en la segunda columna de la Tabla 1. Es decir, el ejercicio de conjeturar una fórmula es la parte más importante de todo este texto. Es la parte que la o lo ayuda a usted. Y créame, es totalmente irrelevante que se le ocurra una fórmula correcta, pero lo que sí importa, es la posibilidad que se le ofrece de imaginar algo nuevo, algo que no pensó nunca antes, algo que la (o lo) hará sentir la potencia de poder pensar... En fin... sigo.
Mientras tanto le propongo que nos detengamos (juntos) a ver si podemos detectar algunos patrones. Fíjese si usted está de acuerdo conmigo.
a) El número 1 aparece ganador cuando hay 1, 2, 4, 8, 16, 32... número de soldados. ¿Qué sugiere esto? Fíjese que estos números son exactamente las primeras potencias de. O sea: 1 = 20, 2 = 21 , 4 = 22, 8 = 23, 16 = 24 , 32 = 25, ....
Ante esta evidencia, uno tiene derecho a conjeturar: ¿será verdad que si el número de soldados es una potencia de dos, entonces el ganador será siempre el número 1? Quiere pensar usted...
Por las dudas: la respuesta es que SI, que eso sucede siempre. Ahora... ¿Por qué pasará esto?
- b) Por otro lado, más allá de lo que sucede con las potencias de dos, fíjese que a medida que se va incrementando el número de soldados, en la columna de la derecha quedan como ‘sobrevivientes’ únicamente números impares (esto en sí mismo no es una sorpresa porque ya sabemos que los primeros eliminados son los pares), pero lo notable es que los impares aparecen todos, sin saltearse ninguno, pero el proceso se detiene justo, justo... cuando uno llega a... ¿Qué le parece a usted que sucede? ¿No tiene ganas de darse un tiempo para pensar? Quizás ese tiempo le sirva para conjeturar alguna fórmula que permita anticipar los resultados que aparecen en la columna de la derecha.
Las preguntas que escribí más arriba son preguntas que me sirvieron a mí, pero no tiene por qué ser el camino que le sirva a usted. En cualquier caso, lo que interesa es poder encontrar alguna fórmula que permita contestar lo que sucedió en el caso original (de 41 soldados) y ver si puede obtener una fórmula más general, para cualquier número de soldados.
Más ideas
Las siguientes ideas son para que las pensemos juntos. Sí, ya sé, no estamos juntos y ni siquiera sé cuál será/sería su respuesta. Pero igual, permítame ‘fantasear’ con que usted está acá cerca.
Como le propuse más arriba, creo que vale la pena atender el caso particular de las potencias de dos. Mirando la Tabla 1 queda claro que en los primeros casos (1, 2, 4, 8, 16, 32) el ganador es el número 1. De acuerdo.. pero, ¿por qué pasa? ¿Pasará también para el resto de las potencias de 2? ¿Qué tienen las potencias de dos que las haga tan particulares?
Mire: tome el número 32. La mitad es 16, que también es una potencia de 2. Y la mitad de 16, es 8, que también es una potencia de 2. Y así siguiendo. El proceso empieza en 32, y pasa por 16, 8, 4, 2 hasta llegar a 1. No es ninguna novedad porque justamente eso pasa únicamente con las potencias de 2. Sin embargo, este hecho, que parece tan obvio, a mí me sirvió para entender y contestar la primera pregunta que planteé más arriba. Fíjese cómo lo podemos usar para el caso 64 que no está en la Tabla 1.
Si uno tiene 64 soldados, los primeros eliminados –como siempre- serán los números pares. Quedan 32 que, como ya sabíamos, iba a ser otra potencia de 2. Pero no solo eso: una vez eliminado el 64 (el último de los pares)... ¿a quién le toca ahora? ¡Le toca al 1! Es decir, ahora quedan 32 (todos los impares) pero el que empieza es el número 1... y ya sabemos que si uno tiene 32 soldados, el que tiene el número 1 (el que empieza)... ¡es el ganador! Bueno, eso es lo que pasa en este caso también. Es decir, si uno tiene 64 soldados, una vez recorrida la primera tanda de eliminados, aparece una situación que ya conocíamos: 32 soldados (una potencia de 2) y también conocemos el ganador: ¡el que empieza! Y como empieza el 1, se confirma lo que sospechábamos: en el caso 64, el ganador también es el número 1.
¿Se da cuenta que esta idea se puede usar siempre? Es decir, ahora que sabemos que cuando inician 64 soldados el número 1 vuelve a ganar, este nuevo dato lo puede usar para la siguiente potencia de 2, o sea, 128. Y lo mismo con todas las que siguen: 256, 512, 1024, etc. Este argumento que usamos es tan poderoso que permite sacar esta conclusión (y léala para ver si está de acuerdo conmigo):
“Si el número de personas involucradas es una potencia de 2, el ganador es el que empieza”
Me importa –mucho— que usted detecte que escribí el que empieza, y no el número 1. ¿Por qué? ¿Quiere pensar usted?
...
1-https://es.wikipedia.org/wiki/Problema_de_Flavio_Josefo y https://matesmates.wordpress.com/2012/01/03/el-problema-de-flavio-josefo/
--------------------------------Para suscribirte con $ 1000/mes al Cohete hace click aquí
Para suscribirte con $ 2500/mes al Cohete hace click aquí
Para suscribirte con $ 5000/mes al Cohete hace click aquí

