El problema del ‘no vidente’

Por Adrián Paenza May 20, 2018

Con la estrategia adecuada, todo problema tiene resolución

Quiero plantear un problema precioso y me apuro a escribir que no es mío, ni se me ocurrió a mí. El atractivo central es que requiere elaborar una estrategia. Por lo tanto, hay que pensar.

Cuando uno lee el enunciado por primera vez, sospecha que el problema no tiene solución. Uno cree que no se va a poder. Y sin embargo, sí se puede.

No se me escapa que se conocen múltiples variantes del problema. Yo elegí una de ellas, la que me interesó a mí, pero créame que buceando en internet hay muchas versiones distintas pero similares conceptualmente.

Una última cosa: si usted tiene la tentación de leer la solución (y no hay ninguna razón para sospechar que yo no haría lo mismo), le sugiero que lo piense antes. Créame que se va a robar a usted misma/o de disfrutar el problema aún en el caso que no se le ocurra nada. Si me permite una sugerencia: no se prive del placer de pensarlo. Vale la pena. Ahora sí, acá voy.

El planteo

Supongamos que usted está mirando a una fila de 150 personas. Es fácil descubrir que están ordenados por altura en forma creciente, de adelante hacia atrás. La persona más baja de los 150 será la que ocupe el primer lugar de la fila y la más alta será la última. Lo curioso es que no hay dos alturas repetidas, de manera tal que el orden es estrictamente creciente.

Dicho esto, un señor no vidente (a quien voy a llamar “A”) , que tiene una altura distinta a la de todos los que están en la hilera, quiere incorporarse a ella, pero respetando las reglas que siguen todos. Es decir, una vez que se ubique, tendrá adelante a una persona más baja que él y por detrás, una persona más alta.

Pero claro, como A no puede ver, para poder encontrar su lugar tendrá que hacer algunas preguntas a quienes ya están ubicados, pero no cualquier tipo de pregunta sino solamente esta: “¿Es usted más alto que yo?”. Y nada más.

Ahora, estas son las reglas.

Todos están forzados a decir la verdad.
A puede formular la pregunta tantas veces como quiera y naturalmente, las dos potenciales respuestas son SI o NO. (Eso sucede porque todos tienen una altura diferente entre ellos, incluso al compararlos con A.)
Nadie puede contestar ‘no sé’. Todos son capaces de comparar su altura con la de cualquier otra persona.

Pero falta algo más. Naturalmente, A podría empezar preguntándole al primero que esté en la fila. Si le contesta que sí (recuerde que lo único que él puede preguntar es ‘¿es usted más alto que yo?’), entonces él se ubicará allí adelante y se terminó todo. Pero también podría suceder que la primera respuesta sea un ‘no’, y entonces, necesita seguir preguntando. Creo que está claro que si A va preguntándole a cada uno siguiendo el orden en el que aparecen en la fila, encontrará su lugar en el primer momento que alguien le diga que ‘sí’. Cuando eso suceda, se ubicará entre el anterior y quien le contestó afirmativamente.

Ya sé lo que usted está pensando: ¿y si nadie le dice que ‘sí’? Bueno, en ese caso, A terminará siendo el más alto de todos y se ubicará en el último lugar.

Pero así planteado, el problema no tiene ninguna gracia. Quiero proponerle otra restricción, que le dará un sabor distinto y le va a proporcionar otro tipo de satisfacción al pensarlo.

Suponga que quien escribió las reglas le dice a A que tiene que poder encontrar su lugar en la fila al escuchar a lo sumo dos respuestas afirmativas. Es decir: puede escuchar que le contesten que ‘no’ incluso 150 veces (si él es el más alto de todos), pero la idea es que él pueda elaborar una estrategia que le permita encontrar dónde ubicarse al escuchar (como máximo) dos veces ‘sí’.

Fíjese que no estoy diciendo que forzosamente tiene que escuchar dos veces que ‘sí’. De hecho, si al preguntarle al primer ubicado en la fila le dijera que sí, lo escuchará una sola vez y no le hará falta nada más: se ubica adelante de todos y listo. Lo que le estoy proponiendo es que en el momento que A escuche el segundo ‘si’, allí no podrá preguntar más. Allí tendrá que haber conseguido la información suficiente y tendrá que poder decidir cuál es el lugar que deberá ocupar en la hilera. El segundo SI indicará el final de las preguntas.

Ahora sí –finalmente– el enunciado del problema:

¿Qué estrategia podría diseñar usted si fuera quien asesora a A, de manera tal que le sirva para encontrar su lugar en la hilera haciendo el mínimo número de preguntas posibles?

Por supuesto, tendrá que respetar las reglas y sin importar cuál sea la distribución de las 150 personas.

Una pausa. Le sugiero que lea el problema con detenimiento porque parece una suerte de trabalenguas cuando en realidad debería ser fácil de entender. Antes de avanzar, convénzase de que entendió qué es lo que hay que hacer, qué estrategia se espera que usted diseñe y qué es lo que le está permitido hacer y qué está prohibido (por ejemplo, hacer alguna pregunta que difiera de la que escribí más arriba, o que obtenga más de dos respuestas afirmativas, por ejemplo).

Una ayuda

Para continuar, quiero ofrecerle yo una parte de la solución. Sí; yo le voy a dar el menor número de preguntas que usted va a necesitar que A formule para estar seguro que no importa cómo sea la relación de la altura de él con las otras 150 personas, él va a encontrar su lugar. Ese número es 17. Sí, diecisiete. Es decir, lo que estoy afirmando acá (y se lo ofrezco como una ayuda) es que haciendo a lo sumo 17 preguntas, usted va a poder determinar cuál debería ser su lugar en la fila.

Algunas preguntas que –creo— le serán útiles:

¿A quiénes les tiene que preguntar?
¿En qué orden?
¿Cómo idear un plan de manera tal que si A lo sigue, entonces seguro que haciendo a lo sumo 17 preguntas encuentre su lugar?

Otras preguntas posibles:

La estrategia que usted elabore, ¿será única o puede haber otras?
En todo caso, ¿no habrá otra forma de diseñar una estrategia de manera que –eventualmente– con menos preguntas A pueda encontrar su lugar?

Como ve, hay muchos interrogantes. Si me permite una última observación antes de dejarla/dejarlo pensar: no se deje ganar por la frustración si no se le ocurre algo de entrada. Intente probando y eventualmente, ‘errando’. No conozco otra forma. Dudo que a alguien se le pueda ocurrir qué hacer sin intentar antes y equivocarse o fallar.

Ahora sí, le toca a usted.

Una respuesta posible

Como escribí acá arriba, no me imagino que una persona que vea este problema por primera vez, pueda intuir qué hacer sin someterse a un juego de ‘prueba y error’. No hablo de lo que me pasó a mí exclusivamente, sino de lo vi que le sucedió a toda persona a quien se lo planteé a lo largo de los años.

Le sugiero que empecemos pensando con números más pequeños, de manera tal de tratar de encontrar alguna idea. A priori, sin reducirlo a una situación más manejable, debería confesar que no se me ocurre nada. Más aún: podría pasar que el señor ciego fuera el más alto o el más bajo. ¿Cómo conciliar esto?

A partir de ahora, en el texto que sigue, voy a suponer que yo soy el señor A.

Es decir, en este trayecto voy a suponer que yo soy la persona no vidente, y me propongo ENCONTRAR mi lugar en la fila, consultando A LO SUMO a 17 personas. Veamos cómo hacer.

Un par de hechos importantes que quiero compartir, y le pido que antes de avanzar se ponga de acuerdo conmigo en que usted comparte lo que voy a escribir.

Suponga que le pregunto a la persona número 40, por elegir un número cualquiera.

Si me contesta que NO, quedan eliminadas las primeras 40 personas. Mi lugar en la fila estará detrás del número 40. Podría ser incluso que no hubiera nadie más alto que yo, en cuyo caso mi lugar sería detrás del 150 (si él fuera el último): yo sería a partir de ese momento el más alto de todos. Eso sí: si el número 40 me contesta que NO, gasté una pregunta PERO no utilicé ninguno de los dos SI que puedo usar para encontrar mi lugar.
Si me contesta que SI, entonces mi lugar en la fila está por delante del 40. Lo que sucede en este caso, es que usé una de las 17 preguntas que puedo hacer, y encima, me gasté uno de los dos SI que puedo escuchar. A partir de este punto, no me queda más alternativa que empezar a preguntar desde el primero de la fila, uno por uno. ¿Por qué? Es que a partir de ahora, cualquier pregunta que haga que tenga una respuesta afirmativa (un SI), yo debería tener toda la información necesaria para saber en qué lugar tengo que ubicarme. Fíjese que si –por ejemplo— después de haber recibido un SI del número 40, yo decidiera preguntarle ahora al número 20 (por poner un ejemplo cualquiera), si me llegara a decir que SI, yo no sabría dónde ubicarme porque lo único nuevo que aprendí es que mi lugar está entre los 19 primeros, o incluso transformarme en el primero, pero no tengo ya más preguntas para hacer para poder determinarlo. Luego, si el número 40 me contesta que SI, me veo forzado a ir hasta la primera persona de la fila y seguir preguntando desde allí. Pero lo que me interesa sugerirle que pensemos es que si bien estoy forzado a preguntarle a la primera persona, usted se da cuenta que me quedan nada más que 16 preguntas (de las 17, ya usé una para el número 40). ¿Qué indicará esto? ¿Será razonable empezar con el número 40? ¿No convendría entonces empezar preguntándole a la persona de la fila tal que si me contestara que SI, con las 16 preguntas que me quedan por hacer yo pueda decidir en qué lugar ubicarme? Y si usted piensa un instante, descubrirá que la persona con la que me conviene empezar las preguntas es con la número 17.

Le pido que relea las partes (a) y (b) que figuran acá arriba, para estar preparado para lo que sigue. Yo elegí el número 40 porque tenía que elegir alguno. Lo podría haber llamado número X, pero preferí el 40 para tener un número concreto.

Ahora sí, empiezo con la estrategia. Le recuerdo que yo tengo 17 preguntas por hacer y hay 150 personas en la fila.

Empiezo así. Le pregunto primero a la persona número 17.

Si me dice que SI, entonces, como hice en la parte (b) que figura acá arriba, tengo que seguir preguntando con el primero de la lista. ¿Por qué? Es que en el peor escenario posible, en el que todos los anteriores (del 1 al 16) me dijeran que no, usé todas las preguntas posibles (las 17), y si todos me contestaron negativamente, entonces mi lugar en la fila es entre el 16 y el 17. Podría ser que algún otro me diga que sí antes pero en ese caso, me tendría que poner adelante de él y por detrás del anterior que me tuvo que haber dicho que no. Por ejemplo, empiezo preguntándole al 1 que me dice que no. Al 2 que me dice que no. Al 3, al 4, al 5... y todos me dicen que no. Supongamos que el número 6 me dice que sí. Esto quiere decir que el 6 es más alto que yo, pero el 5 me había dicho que no. Mi lugar entonces es entre el 5 y el 6. Fíjese que encontré mi lugar usando 17 preguntas o menos (en este último caso hubieran sido siete preguntas: al 17, al 1, 2, 3, 4, 5 y 6, y en el momento que escuché el segundo SI, ya supe en qué lugar me tenía que ubicar.
Si el número 17 me dice que NO, entonces lo único que pasó es que me gasté una pregunta de las 17 posibles, pero todavía sigo conservando los dos SI, ya que no escuché ninguno todavía.

¿A quién preguntarle ahora? ¿Quiere pensar usted? Fíjese que usé nada más que una pregunta y tengo todavía a mi disposición los dos “SI”. Supongamos (por probar con un número cualquiera) que elijo el número 70. Si me dijera que NO, me viene bárbaro porque si bien usé en total dos preguntas, con ellas eliminé 70 personas. Si llegara a haber alguien más alto que yo, tiene que estar después del 70.

Pero, ¿si el 70 me llegara a decir que SI? Entonces estoy con un problema serio, porque, por un lado, ya usé dos preguntas de las 17 que tengo, y por otro, como escribí más arriba (en la parte (b)), la próxima pregunta la tengo que hacer al número 18 ya que la primera persona más alta que yo tiene que ser alguien que esté ubicado detrás del 17 y antes del 70. Pero yo tengo nada más que 15 preguntas para hacer por lo que claramente, si todos me fueran diciendo que NO, yo llegaría hasta el número 32 (desde el 18 hasta el 32 hay 15 preguntas aunque parezcan 14... verifíquelo usted). Por lo tanto, si hasta el 32 me dijeron todos que NO, me gasté todas las preguntas que tenía y sigo sin saber mi lugar.

Luego, haber ‘saltado’ desde el 17 al 70 no fue una buena decisión. Sabiendo que cuando haga la siguiente pregunta, si me contestaran que SI me quedan nada más que 15 por hacer, debería hacérsela a alguien que me permita cubrir todo el espectro que va entre 18 (que es donde tengo que empezar a preguntar) y el siguiente que resulte de sumar (18 + 15) = 33.

Y este dato es muy importante, ya que me dice que con 15 preguntas, como yo voy a tener que empezar en el número 18, puedo llegar hasta el 32. ¿Moraleja? La siguiente pregunta (si el 17 me dice que NO), es hacérsela al 33. Si el 33 me dice que NO, ya veré cómo sigo, pero si me dice que sí, empiezo preguntándole al 18 y me quedan justo 15 preguntas para cubrir todas las posibilidades hasta el 32 por lo que seguro que voy a descubrir mi lugar en la fila.

Como usted detecta, si el 33 me dijera que no, el siguiente debería ser... (¿quiere pensar usted?) ...Sí, el 48. ¿Por qué? Porque si me dice que NO, ya tenemos una idea de cómo seguir (llegando hasta el 62, que resulta de sumar 14 al 48, que es el número de preguntas que me van a quedar). Si me contesta que SI, entonces uso las 14 preguntas empezando desde el 34 y con esas 14 preguntas llego hasta el 47, que es lo que necesito.

Y creo que a esta altura usted ya ha descubierto cuál es el patrón que voy a usar tanto en el caso que me contesten que SI o que NO.

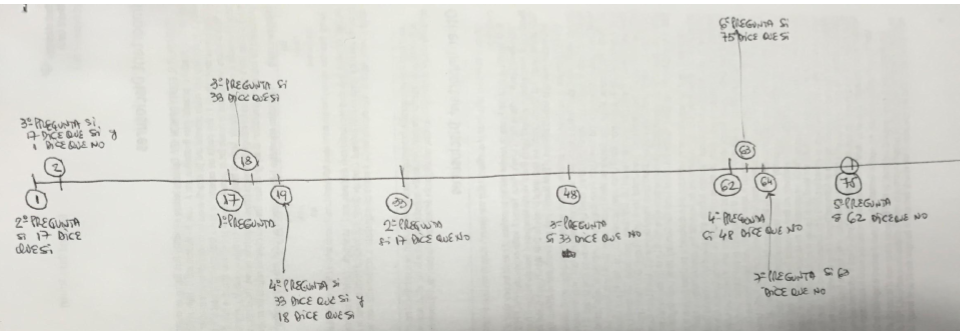
Resumo lo que vimos hasta acá: empecé preguntando al 17, después al 33 (que son 16 más), después al 48 (que son 15 más), después al 62 (que son 14 más), y sigo con estos: 75, 87, 98, 108, 117, 125, 132, 138, 143, 147, 150, 152 y 153.

¿Qué conclusiones podemos sacar?

La primera es que si me llegaran a contestar todos que no, con las 17 preguntas que tenía inicialmente llego a cubrir hasta –incluso más que– el 150. De hecho, llego hasta el 153.

Si en alguno de los pasos intermedios alguno de ellos me contestara que SI, el número de preguntas que me queda a esa altura, es exactamente el que necesito para ir para atrás y empezar preguntando a uno por uno.

Es decir, es una buena estrategia, porque agoto todos los casos que se me pudieran presentar. Está claro que puede que no necesite usar las 17 preguntas e incluso que no necesite llegar a escuchar los dos SI. De hecho, podría ser que no escuche ningún SI. Esto podría pasar si yo fuera el más alto de todos.

Ahora bien. No quiero terminar sin mostrar que con menos de 17 preguntas puede que no llegue a determinar mi lugar en la fila.

Supongamos que tuviera 16 preguntas por hacer.

Empiezo en el número 16 y voy haciendo como antes, sumas que vayan disminuyendo en uno. Las personas a las que les preguntaría son:

16, 31, 45, 58, 70, 81, 91, 100, 108, 115, 121, 126, 130, 133, 135, 136.

Es decir, con menos de 17 preguntas, no llego a cubrir las 150 personas que tengo que investigar.

Y esto termina el análisis. Hemos encontrado una estrategia que funciona con las 17 preguntas y cumpliendo con la otra restricción respecto del número de respuestas afirmativas que puedo escuchar en el camino.

Apéndice 1

Como usted habrá observado, con las 17 preguntas no solo alcanzaría para cubrir las 150 personas, sino alcanzarían para encontrar mi ubicación entre 153. Por lo tanto, al margen de empezar con el número 17, es posible empezar preguntando a otras personas y el resultado sería el mismo. Acá van todas las posibilidades.

a) 17, 33, 48, 62, 75, 87, 98, 108, 117, 125, 132, 138, 143, 147, 150
b) 16, 32, 47, 61, 74, 86, 97, 107, 116, 124, 131, 137, 142, 146, 149, 150
c) 15, 31, 46, 60, 73, 85, 96, 106, 115, 123, 130, 136, 141, 145, 148, 149, 150.
d) 14, 30, 45, 59, 72, 84, 95, 105, 114, 122, 129, 135, 140, 144, 147, 149, 150.

Apéndice 2

Otras preguntas que uno podría contestar y que sirven para entender por qué hacen falta 17 preguntas si uno tiene 150 personas.

Fíjese en lo siguiente que involucra un razonamiento ‘inductivo’. Voy a empezar primero con una sola pregunta y voy a mostrar (en el caso más fácil) que si hay una persona en la hilera, yo voy a poder encontrar mi lugar

Ahora aumentemos el número de preguntas y supongamos que ahora puedo hacer dos. Vamos a encontrar una estrategia que permita encontrar mi lugar en la fila si hay tres personas. Después, vamos a aumentar el número de preguntas y permitir hasta tres. En ese caso, vamos a convencernos que puedo tener hasta seis personas y con esas tres preguntas voy a descubrir mi lugar.

Y voy a seguir, aumentando cada vez más el número de preguntas pero también eso nos va a permitir aumentar también el número de personas que puede haber en la fila.

Ahora sí, acompáñeme por acá porque el argumento que voy a usar repetidamente, se usa MUCHISIMO en matemática.

Primer caso: Como decía, empiezo por la situación más sencilla de todas. Si me dejaran hacer nada más que una pregunta, ¿cuántas personas puede haber en la fila? Como es fácil ver, con una sola pregunta puedo resolver el caso que haya una sola persona. Voy, le hago la única pregunta que puedo (“¿es usted más alto que yo?”) y listo. Si me dice que sí, me ubico delante de él. Si me dice que no, me ubico detrás.

Un paso más: ¿podría encontrar mi lugar si tuviera una sola pregunta por hacer y hubiera dos personas en la fila? Fíjese que no se va a poder. ¿Por qué? Supongamos que le preguntara a la primera persona. Si me dijera que sí, que es más alto que yo, no hay problema. Me coloco delante de él y listo. Pero, ¿si me dice que no? Entonces, no sabría si la segunda persona es más alta que yo o no, y ya no me quedan más preguntas para hacer. Por otro lado, si le preguntara primero a la segunda persona, si me dijera que no, entonces resuelvo el problema. Me ubico detrás de él (porque yo sería el más alto) y listo. Pero, ¿y si me contestara que sí? ¿Qué hago? Porque ya no tengo más preguntas, y no sé si yo soy más alto o más bajo que el primero.

Moraleja: con una pregunta solamente puedo resolver el problema si en la fila hay nada más que una sola persona.

Segundo caso: supongamos que me permiten hacer dos preguntas. Voy a mostrar acá que puedo encontrar mi ubicación si hay tres personas. ¿Cómo hago?

No me conviene preguntarle a la primera persona de entrada, porque –como antes— si me contesta que sí, que es más alta que yo, me ubico delante de él y listo. Pero si me dice que no, me queda una sola pregunta y tengo que ubicarme en una fila que ahora tiene dos personas (la segunda y la tercera). Por lo que vimos más arriba, con una sola pregunta y dos personas puede que no me pueda ubicar. Luego, preguntarle a la primera no es una buena idea.

Por razones simétricas, no me conviene empezar por la última. (Le sugiero que lo piense usted para convencerse de que lo que estoy escribiendo es cierto.)

Sigo yo. Si le preguntara a la última (la tercera persona), entonces si me dice que no, que no es más alto que yo, resuelvo la situación porque me ubico último. Pero si me dijera que sí, que es más alto que yo, se me presenta una vez más la situación anterior: me queda una sola pregunta por hacer y una fila de dos personas para encontrar mi lugar: la primera y la segunda. Luego, empezar por la tercera persona tampoco es una buena idea.

Fíjese que en ambos casos utilicé el hecho que mostré más arriba que era cierto: con una sola pregunta ¡no puedo resolver el caso de dos personas!

Ahora voy a tratar de convencerla/convencerlo, que si le pregunto a la persona que está en el medio, es decir a la segunda, entonces SI voy a poder encontrar mi ubicación. Si al preguntarle a la segunda persona me contesta que sí, entonces, me queda una pregunta y una sola persona (la primera) para decidir donde ubicarme. Este caso, ya sabemos que lo puedo resolver (aunque en este caso uno tenga la tentación de hacer el análisis nuevamente). Por otro lado, si la segunda persona me dijera que no, que no es más alto que yo, entonces otra vez, me queda una pregunta para usar y una sola persona para ubicarme. Ya sé que lo puedo resolver.

Moraleja: con dos preguntas puedo encontrar mi lugar en una fila de tres personas.

Con dos preguntas y cuatro personas, ya no voy a poder. ¿Por qué? (le sugiero que haga el análisis usted, pero verá que empiece donde empiece, se tropezará con la siguiente dificultad en algún momento: tendrá una sola pregunta, y dos personas para encontrar su ubicación, y ya sabemos que eso no se puede resolver). Luego, con dos preguntas, puedo encontrar mi ubicación siempre si en total hay tres personas.

Siguiente caso. Supongamos que me dejan hacer tres preguntas. Quiero convencerla/lo que ahora se pueden tener hasta seis personas. Veamos cómo, y le sugiero que empecemos a buscar un patrón que después nos va a servir para los casos que siguen.

Si uno tiene seis personas y puede hacer tres preguntas, empieza preguntándole a la tercera. Si contesta que SI, entonces tengo dos preguntas más y dos personas (que son las que están delante de la tercera, la primera y la segunda) para encontrar mi ubicación. Por lo que vimos antes, seguro que puedo. Si la tercera persona me llegara a contestar que NO, entonces me quedan dos preguntas y tres personas para encontrar mi ubicación (la cuarta, quinta y sexta), pero lo bueno es que nosotros ya sabemos que con dos preguntas puedo encontrar mi ubicación cuando hay tres personas.

Moraleja: con tres preguntas, puedo encontrar mi lugar entre seis personas.

Breve resumen hasta acá.

Con una pregunta - Encuentro mi lugar si hay una persona

Con dos preguntas - Encuentro mi lugar si hay tres personas (preguntándole a la segunda persona)

Con tres preguntas - Encuentro mi lugar si hay seis personas (preguntándole primero a la tercera persona)

Como usted se imagina, si uno tiene ahora cuatro preguntas para utilizar, ¿cuántas personas le parece que podrá haber en la fila? Sí, lo que usted conjetura es correcto: pueden haber hasta diez personas.

¿A quién preguntarle primero? Como era esperable también, a la cuarta persona. ¿Por qué a la cuarta? Porque si me contesta que sí, que es más alta que yo, me quedan tres preguntas (que me sobran eventualmente) para ubicarme entre las primeras tres personas. Pero si me contesta que no, entonces me quedan tres preguntas y seis personas (que son las que están detrás de la cuarta: la quinta, sexta, séptima, octava, novena y décima). Y ya sabemos por los casos anteriores, que con tres preguntas me puedo ubicar entre seis personas. Y listo.

Con cinco preguntas, puedo encontrar mi lugar entre 15 personas. ¿Por qué 15? Porque 15 = 1 + 2 + 3 + 4 + 5. ¿Y a qué persona preguntarle primero? A la quinta. Si me dijera que SI, que es más alta que yo, tengo cuatro preguntas para ubicarme entre los cuatro primero y si me dijera que NO, me quedan cuatro preguntas para los diez que tiene detrás, situación que recién resolvimos.

Como usted detecta, el patrón que se obtiene es el siguiente:

¿Cuál es la moraleja entonces? Que con 17 preguntas, uno puede encontrar su ubicación –como máximo— entre 153 personas. Por lo tanto, si en la fila había 150, seguro que con las 17 preguntas me voy a ubicar.

Apéndice 3

Si usted revisa ahora el Apéndice 1, verá que fui decreciendo hasta llegar a empezar con el 14. No podría empezar con el número 13, porque quedarían 16 preguntas por hacer y 137 personas, y como vimos más arriba, con 16 preguntas puedo encontrar mi ubicación entre 136 personas y no 137.

Y esto completa el análisis total.

--------------------------------

Para suscribirte con $ 1000/mes al Cohete hace click aquí

Para suscribirte con $ 2500/mes al Cohete hace click aquí

Para suscribirte con $ 5000/mes al Cohete hace click aquí