El reloj de dos colores

 

El que sigue es un problema precioso para pensar porque ‘a priori’, parece que no se podrá, o mejor dicho, es anti-intuitivo. Me explico. Suponga que usted tiene un reloj de pared, cualquiera. De momento, supongamos que es un círculo con 12 lugares (en donde normalmente ubicaríamos a los 12 números en donde el reloj marca las horas).

Yo le entrego dos lápices de dos colores diferentes, digamos rojo y azul. Le doy la libertad que pinte la mitad de cada color, como usted quiera. La única condición es que haya seis pintados de rojo y seis pintados de azul.

Lo que quiero, es convencerla/o de que haga lo que haga, los pinte como los pinte, seguro que yo puedo trazar un segmento que corte al reloj por la mitad, de manera tal que en una mitad hay tres rojos y tres azules (y naturalmente, lo mismo sucederá en la otra mitad). Usted, ¿qué cree que va a pasar? ¿Se podrá o no?

¿Quiere intentarlo?

 

 

Idea para la solución

No sé lo que le pasó a usted, pero yo, cuando vi el problema me pareció que no era posible, o mejor dicho, me pareció que yo estaría en condiciones de pintarlo de alguna forma de manera tal que ningún corte dejaría las dos mitades con la misma cantidad de rojos que de azules. ¿Se podría?

Hagamos lo siguiente y le voy a mostrar por qué siempre se puede. Usted, empiece pintándolos como quiera. Cuando haya terminado, yo tomo una regla y trazo un segmento que corta el reloj por la mitad de cualquier forma. No tengo la expectativa de tener éxito, es decir, sería una casualidad total que yo lo cortara al azar produjera lo que espero que pase. De hecho, si justo llegué a encontrar que hay tres de cada color, se terminó el problema.

Entonces, supongamos que no, que hay 4 rojos y 2 azules (por elegir un ejemplo cualquiera). Esto quiere decir que en su mitad, hay al revés: 2 rojos y 4 azules.

Ahora, yo voy a mover la línea que recién tracé en el sentido de las agujas del reloj. Es decir, voy a producir un nuevo corte por lo que como usted advierte aparecerá un círculo nuevo que no estaba antes, pero al mismo tiempo, desaparecerá otro.

Hay tres posibilidades al mover la línea. (¿Quiere pensarlas usted? Después podemos confrontar si estamos de acuerdo.) ¿Cuáles son los tres posibles casos? Piense también que cualquier modificación que yo produzca en ‘mi’ mitad, impacta en los seis círculos suyos. Si yo pierdo un rojo, lo gana usted. Si yo gano un azul, lo pierde usted. Es decir, estamos interconectados. Ahora, veamos qué sucede en cada uno de los tres casos posibles:

1. Si el que agregué es del mismo color del que perdí no cambia nada. Yo seguiré teniendo en mi mitad 4 rojos y 2 azules (y usted, al revés).
2. Si yo agrego un azul y pierdo un rojo, en este caso, se termina el problema, porque yo tengo ahora 3 rojos y 3 azules, y lo mismo le pasa a usted. Esta situación sería ideal porque conseguiría lo que me había propuesto. Y de paso, usted también.
3. La última posibilidad es que yo agregue otro rojo y pierda un azul. En ese caso ahora tengo 5 rojos y 1 azul, y usted, al revés.

Tengo dos observaciones que me parecen importantes y le pido que me acompañe en estos razonamientos.

• Yo podría seguir analizando los casos que se producen cada vez que vaya moviendo la línea, pero como usted advierte, si yo sigo haciendo esto (independientemente de lo que vaya sucediendo con los colores que gane o que pierda), llegará un momento en el que yo pasaré a estar en la situación que estaba usted al principio, y viceversa (usted estará en al mía). ¿Me sigue? Al mover la línea seis veces, será equivalente a intercambiar nuestras posiciones iniciales.
• Por último —y esto es muy importante— en cada paso yo no puedo más que agregar o perder un color. No puedo agregar dos rojos por ejemplo, ni dos azules. Toda modificación se hace por pasos de a uno. O bien agrego un rojo o bien agrego un azul, o eventualmente, no cambio nada, pero no puedo ganar dos rojos en una sola movida de la línea (ni perderlos).

Con toda esta información, fíjese que si yo empecé con 4 rojos y 2 azules, y lo peor que me pudo pasar es que al ir moviendo la línea yo nunca llegué a tener 3 rojos y 3 azules, quiere decir que en algún momento llego a estar en SU posición inicial. Pero usted empezó con 4 azules y 2 rojos. Para que yo haya llegado a estar en su lugar, como no pude saltar de 4 rojos (los que tenía yo al principio) a tener 2 rojos (como los que tenía usted al principio), esto significa que en algún momento tuve que haber pasado por tener 3 rojos (y por ende tres azules). Y en ese momento justo, usted tenía lo mismo que yo: 3 rojos y 3 azules.

 

 

Moraleja

¿Qué nos enseña esto? Esto muestra que inexorablemente hubo algún momento en el movimiento de la recta que pasé por la situación que quería. ¡Y allí hubiera debido terminar el problema!

 

 

Apéndices

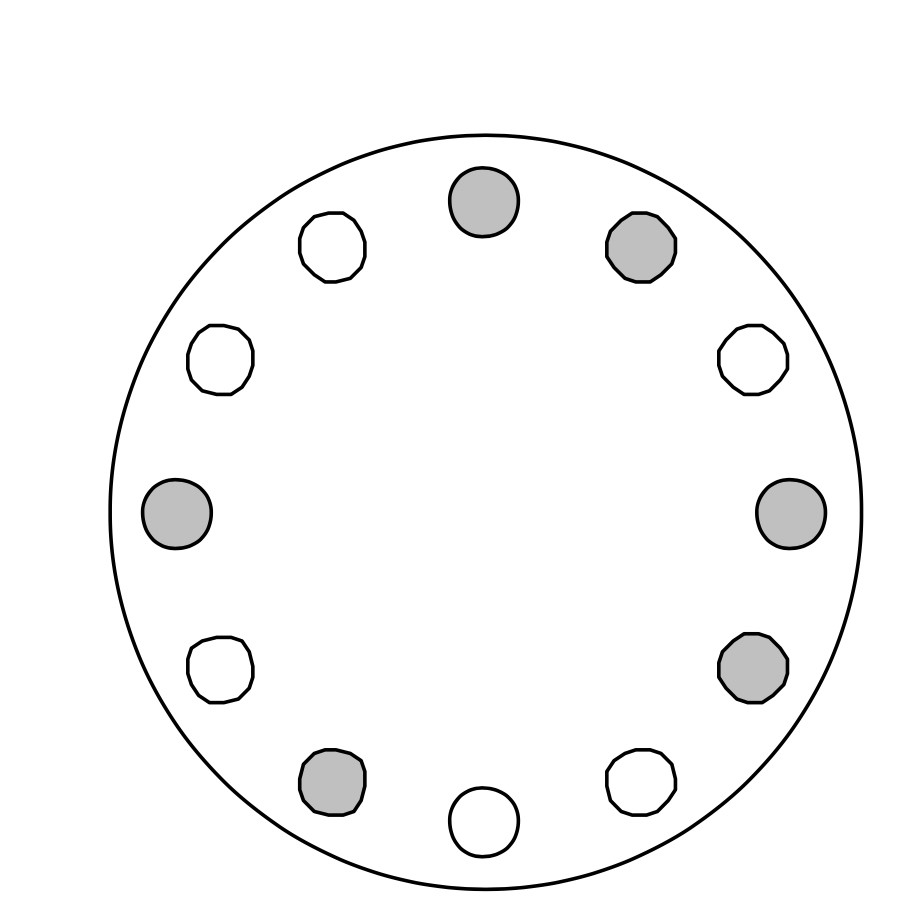
• Voy a poner acá un ejemplo más visual, para poder entender lo que fui describiendo arriba paso a paso. Voy a elegir una forma cualquiera de pintarlos, como se ve en la Figura 1. Ahora quedaron pintados de gris y de blanco.

 

 

 

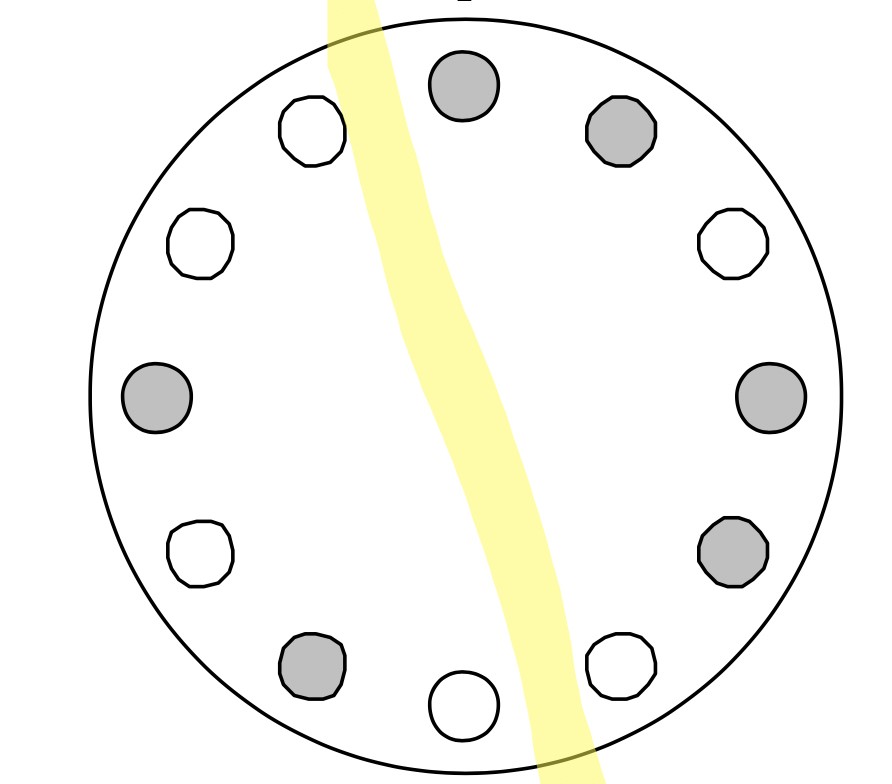
Elegí una forma cualquiera de cortar. A la izquierda, en mi mitad, quedaron cuatro blancos y dos grises.

Ahora, empiezo a rotar la línea que corta. Restulta entonces esta nueva figura, la Figura 3:

 

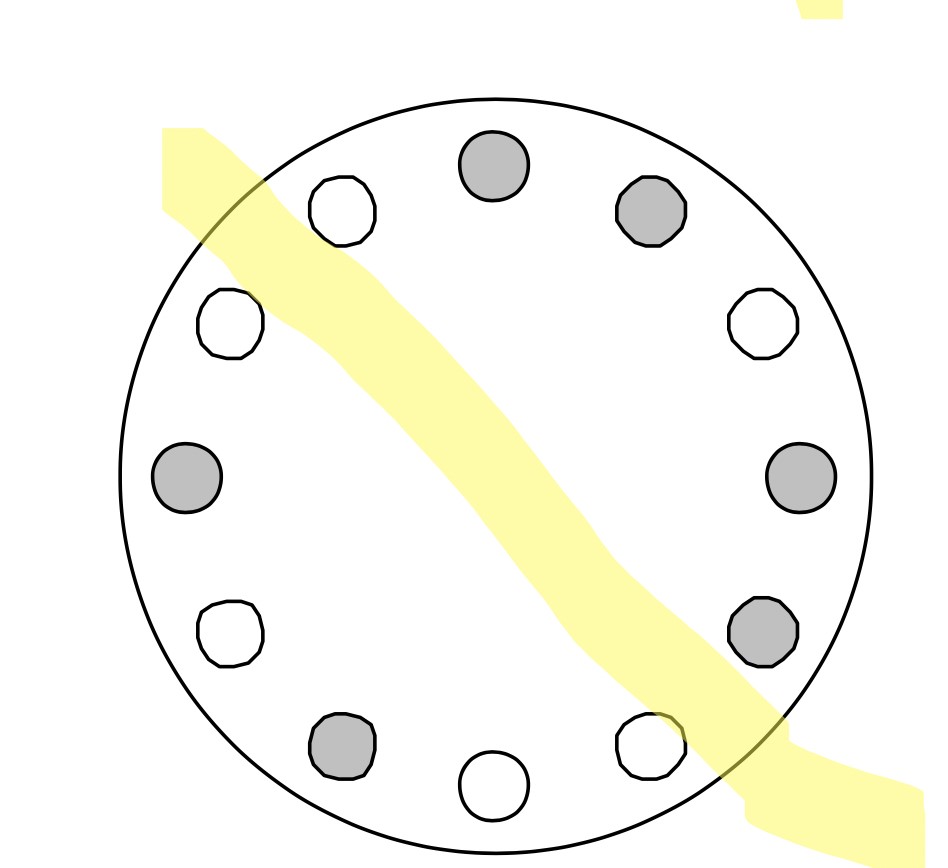
No cambió nada, porque al rotar, perdí un blanco arriba, pero lo perdí abajo. Sigo teniendo cuatro blancos y dos grises (y naturalmente, la otra mitad, sigue teniendo cuatro grises y dos blancos). Vuelvo a rotar la línea, y ahora se obtiene la Figura 4.

 

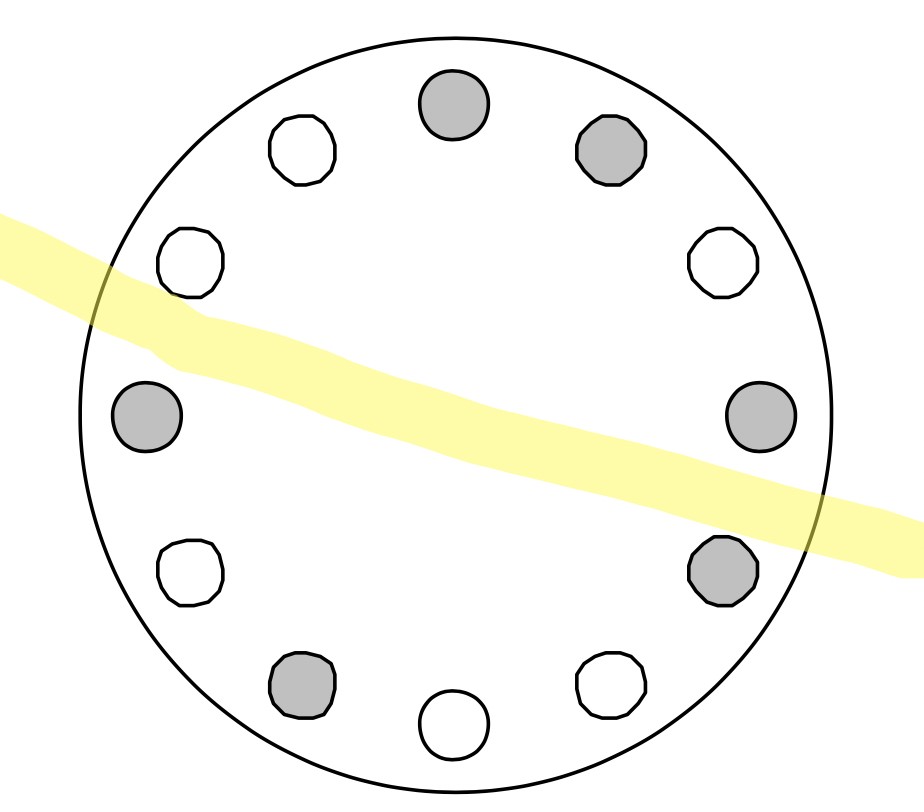
Ahora sí se produjo una modificación. Ahora yo perdí un blanco y gané un gris. En este momento, en mi mitad, tengo tres blancos y tres grises (que es lo que quería). Por otro lado, en su mitad, pasó lo mismo: ahora usted perdió uno de los grises que tenía de más, pero ganó un blanco. Y listo.

Para terminar, quiero proponerle pensar algo más: ¿le parece que tuvo importancia que fueran 12 círculos? Es decir, si en lugar de haber tenido 12 hubiera tenido 400, y los hubiera pintado de alguna forma 200 blancos y 200 grises, creo que con esta idea usted debe (o debería) estar en condiciones de sacar una conclusión más general. ¿Qué debería decir esta conclusión general? ¿Quiere pensar usted? Es que la conclusión debería decir que uno puede garantizar que independientemente de la forma en la que una persona distribuya los colores (por mitades) entre los 400 puntos, seguro que existe una forma de dividir el ‘reloj’ en dos partes iguales, de manera tal que los colores queden distribuidos por mitades también. Y por supuesto, el número 400 también es arbitrario. Cualquiera sea el número par de círculos, el resultado sigue vigente.

El crédito de este problema hay que adjudicárselo a la gente del diario El País de España, quien publicó una serie de problemas de matemática no solo en su versión impresa, sino también digital, aprovechando la extraordinaria plataforma que ofrece tener un diario de tremenda penetración en el mundo hispano-parlante, para promover y proponer problemas de este tipo. Sirva este caso como reconocimiento a lo que hicieron (y hacen) las autoridades del diario El País y los editores que produjeron una serie inolvidable.

 

 

 

 

--------------------------------

Para suscribirte con $ 1000/mes al Cohete hace click aquí

Para suscribirte con $ 2500/mes al Cohete hace click aquí

Para suscribirte con $ 5000/mes al Cohete hace click aquí