La paradoja de Braess

 

Lo que sigue es una historia real. Sucedió en varias partes del mundo casi al mismo tiempo y sobre todo con la aparición de las diferentes redes de autopistas que conectaban no solo países sino también continentes. Por supuesto, mucho tuvo que ver la Segunda Guerra, pero esa es otra historia.

Para ofrecer un contexto razonable, voy a empezar con un ejemplo. Si yo le preguntara en qué lugar del mundo se produce anualmente la mayor concentración de personas, creo que entre los tres primeros sitios estará Times Square, en New York. Es fácil transportarse imaginariamente a cualquier escena nocturna que haya vivido en una película, en fotos o como testigo presencial, de la intersección de la calle 42 y Broadway. En realidad es la intersección de dos avenidas, ya que la 42 es esencialmente una avenida. Pero lo que me interesa es pulsarle una cuerda interna y sugerirle que piense en cualquier escena nocturna en donde los carteles luminosos transforman la noche en día.

Naturalmente, por ese sitio no solo hay personas que caminan y turistas que se juntan para sacar fotos que registren su presencia en el lugar, sino que también hay tránsito vehicular. No hace falta que escriba (pero igual lo hago), que así como hay una enorme presión peatonal, también hay un enorme flujo de tránsito. Ahora bien: ¿qué pasaría si por alguna razón esa avenida/calle, la 42, tuviera que ser bloqueada?

Aunque no estemos juntos, intuyo que la respuesta más esperable será: ¡el tránsito se convertiría en un verdadero caos! Algo así como si bloqueáramos varias cuadras de la calle Corrientes en Buenos Aires, o el boulevard Oroño en Rosario o la avenida Maipú en Córdoba (por poner tres ejemplos cualesquiera, pero usted elija la arteria que le resulte más cercana a su entorno): si uno clausurara o cerrara una calle de esas características, la conclusión que uno sacaría es que se generaría un caos en el tránsito de enormes proporciones.

Sin embargo, y a este punto querría llegar, eso... ¡no pasó! Ni pasa. Hay tres casos muy puntuales que fueron los que llamaron la atención. Uno es el que acabo de escribir sobre la calle 42 en Manhattan, otro es la calle Main en Boston y el tercero sucedió en el barrio de Islington en Londres. Cuando cada una de las tres arterias tuvo que ser temporariamente cerrada, el tránsito, en lugar de empeorar... ¡mejoró!

 

 

Allí aparece en escena un matemático alemán, Dietrich Braess, quien en 1968 presentó su teoría que hoy es conocida como la Paradoja de Braess. Braess era profesor en la Universidad de Ruhr en lo que todavía era Alemania Occidental, y su paradoja dice lo siguiente:

“El simple hecho de agregar un camino a una ruta que habitualmente ya está congestionada de tránsito, no garantiza que el tránsito fluirá mejor ni que se acortarán los tiempos, sino que es posible que suceda exactamente lo contrario, y el nuevo camino sólo sirva para empeorar la situación”

Si usted me acompaña, y tiene la paciencia necesaria para seguir los argumentos que él expuso, verá que si bien es fuertemente antiintuitivo o si usted prefiere, atenta fuertemente contra la intuición que tanto usted como yo tenemos, la explicación de Braess es muy interesante y muy pertinente.

Eso sí: yo voy a ir escribiendo un texto y simultáneamente le propongo que recorra las figuras que lo acompañan. Y por otro lado, le sugiero también que haga usted las cuentas (aunque no es imprescindible porque las voy a hacer yo también), pero la única manera de convencerse de que uno entiende lo que lee es detenerse un rato y ‘equivocarse’ uno o, si prefiere, ‘mancharse las manos’ o ‘engrasárselas un poco’.

Acá voy.

Suponga que usted viaja todos los días desde un punto INICIAL hasta llegar a un punto FINAL. En definitiva sólo se trata de unir dos puntos.

En la Figura 1, hice un pequeño esquema para graficar lo que quiero decir.

 

 

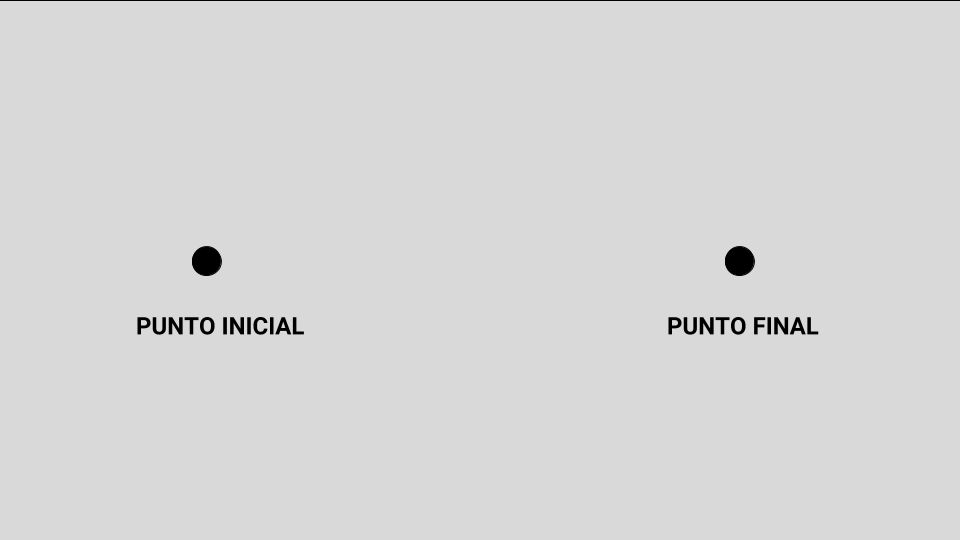
Ahora, pase a la Figura 2. Fíjese en ella y después vuelva a este texto.

 

 

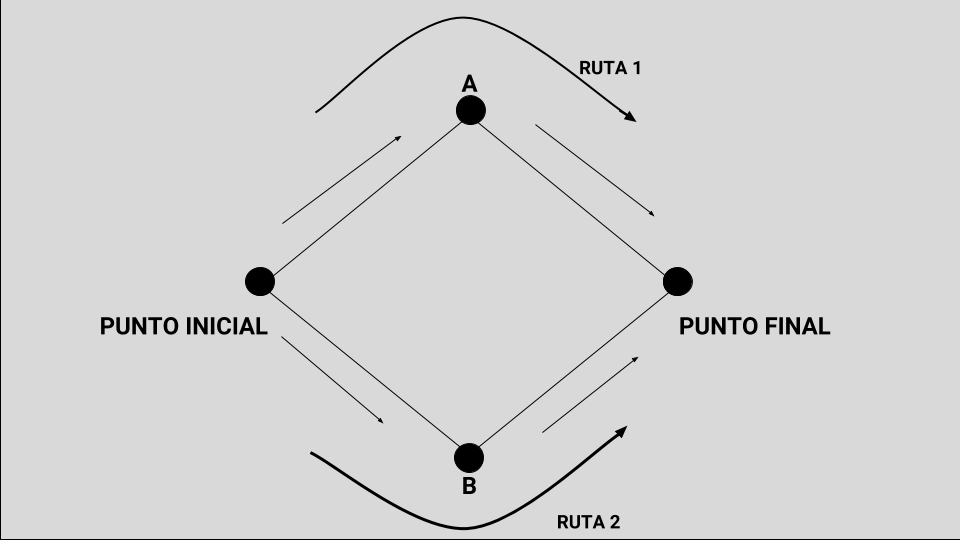
Como se ve, hay dos caminos posibles para ir desde el punto Inicial hasta el punto Final: tomando por la ruta (que voy a llamar Ruta 1), que desemboca en el punto A, y después, desde A hasta el punto Final , o bien, tomando el camino que va desde el punto Inicial hasta B, y desde allí hasta el punto Final, y que voy a llamar, Ruta 2.

Los caminos tienen exactamente la misma longitud de manera tal que elegir uno u otro debería ser totalmente indiferente. El único problema lo genera el tránsito que circula por ambas rutas. Acá es donde empiezo a necesitar de su cooperación. Voy a hacer un ejemplo que involucra a 1000 automóviles o vehículos. Es decir, la idea es establecer un modelo que permita imaginar qué camino van (o pueden) elegir esos mil vehículos para ir desde el punto Inicial hasta el punto Final.

Ahora pase a la Figura 3.

 

 

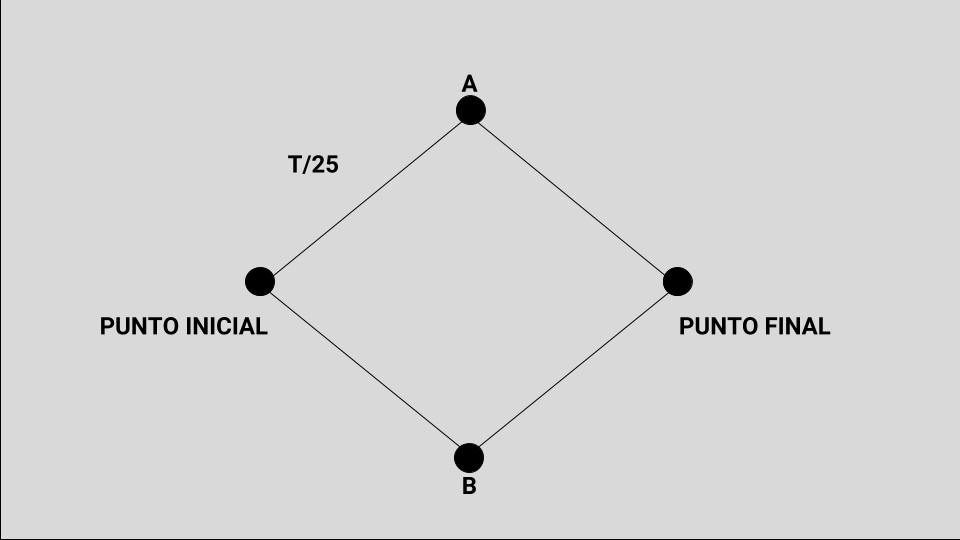
Cuando un auto está parado en el punto Inicial y antes de tomar la decisión de cuál de los dos caminos va a elegir, los datos recogidos a través de las diferentes mediciones indican que si elige el camino que lo lleva hasta A, el tiempo que va a tardar está medido en T/25 minutos, en donde T indica el número de vehículos que eligió ese camino. Por ejemplo, si los 1000 autos eligieran ese camino, como (1000/25) = 40 , esto indicaría que los 1000 autos tardarían 40 minutos –en promedio— en hacer ese recorrido para llegar hasta A. En cambio, si en lugar de tener 1000 autos en esa ruta, solamente 500 lo hubieran elegido, entonces el camino se puede hacer en (500/25) = 20 minutos. Como se ve, el número de autos que elijan un camino es determinante para definir el tiempo que va a consumir el trayecto.

Una vez que uno llegó hasta A, el segundo trecho uno lo hace por una autopista que tiene tantos carriles que el número de vehículos que la recorren no altera el tiempo. En consecuencia, el tiempo no depende más del número de autos, ya que la autopista tolera perfectamente el tránsito de 1000 vehículos sin producir ningún tipo de demora. Como se ve en la Figura 4, supongamos que ese tiempo está fijo y que es exactamente de 50 minutos.

 

 

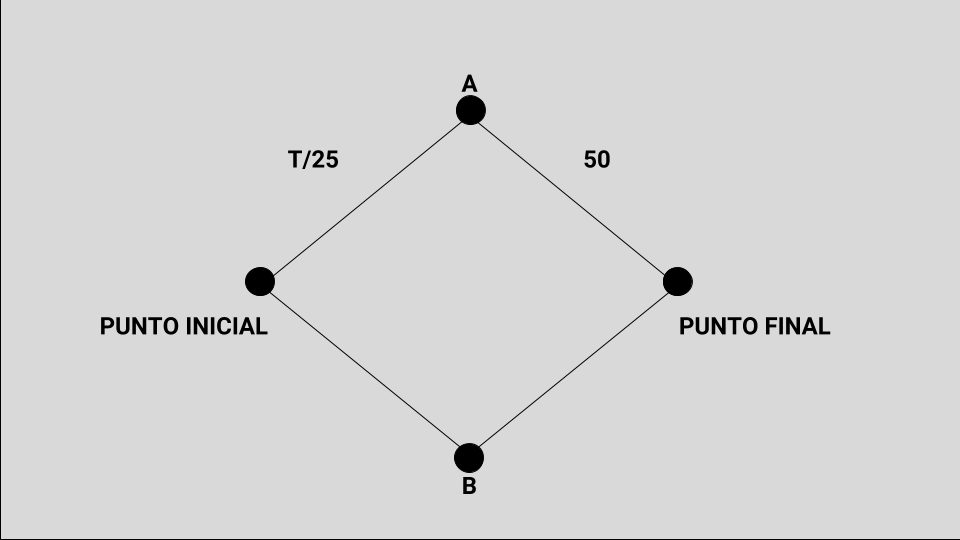
Resumiendo: el primer tramo, lleva T/25 minutos, dependiendo de T, el número de vehículos que lo están recorriendo y el segundo, 50 minutos independientemente de cuántos vehículos la circulen.

Fíjese ahora en la Figura 5.

 

 

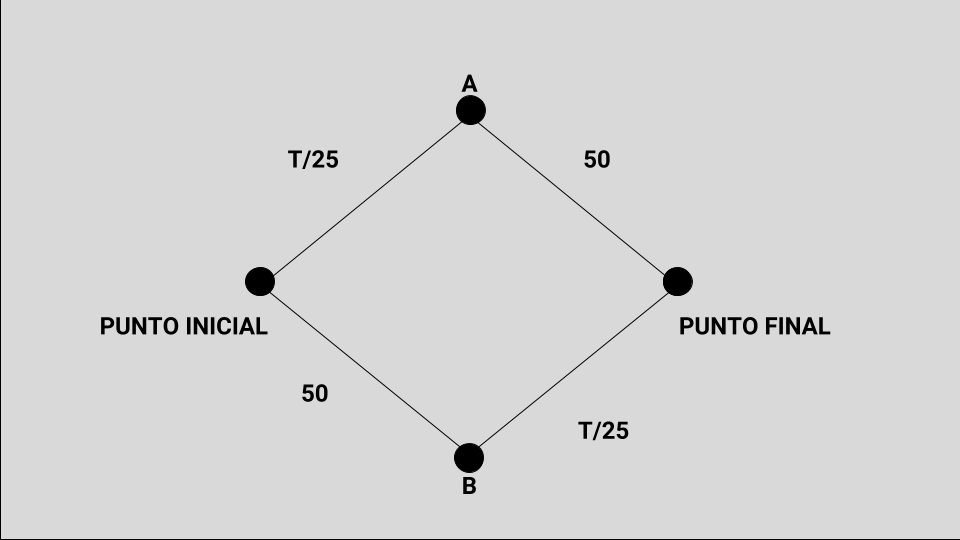
Ahora agregué al esquema la Ruta 2. La situación está revertida ahora. El primer tramo, el que va desde el punto Inicial hasta B no depende del número de vehículos, sino que uno tarda siempre 50 minutos. La dificultad aparece en la segunda parte: allí, el número de vehículos vuelve a adquirir importancia, y el tiempo para recorrerlo se estima –una vez más— en T/25 minutos, como sucedía en la ruta anterior.

Justamente la Figura 5 resume las dos situaciones: ir por el camino que pasa por A y la otra posibilidad, es que elegir el tramo que pasa por B.

Ruta 1:  T/25 minutos + 50 minutos

Ruta 2:   50 minutos + T/25 minutos

Aquí detengámonos y hagamos hipótesis sobre lo que sucedería si imaginamos diferentes escenarios. Digo, qué variaciones habría si más vehículos eligen la Ruta 1 que la Ruta 2 (y viceversa).

Supongamos por ejemplo que hay 600 vehículos que van por la Ruta 1 y 400 por la Ruta 2. En ese caso (Figura 6), tenemos:

Ruta 1: 600/25 + 50 = 24 + 50 = 74 minutos

Ruta 2: 50 + 400/25 = 50 + 16 = 66 minutos

 

 

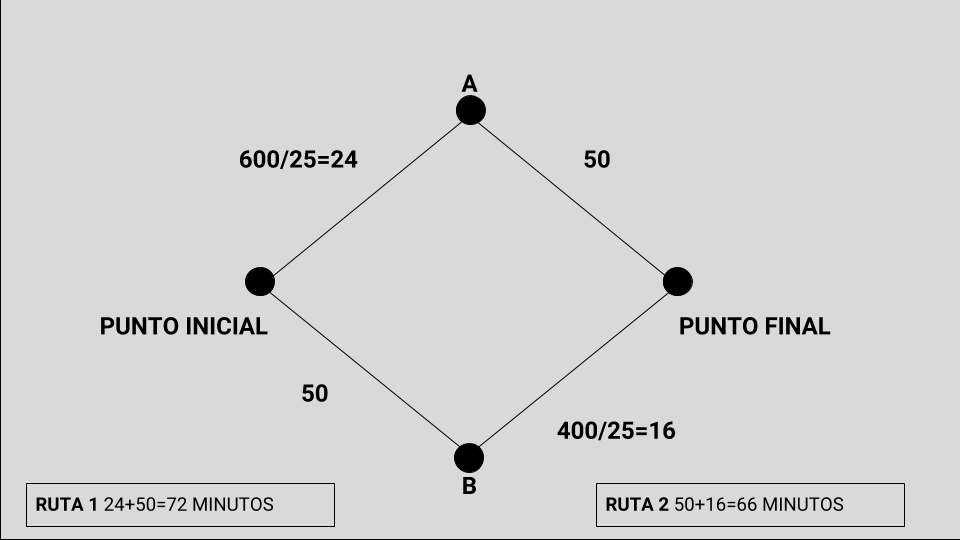
Naturalmente, usando la información que proveen los GPS los vehículos que habían elegido la Ruta 1 (y tardaron 74 minutos), sabrían casi inmediatamente que los que van (o fueron) por el otro lado, tardaron 66 minutos. Como usted se imagina, en poco tiempo, en pocos días, todo el mundo que circula por esas rutas sabría lo que sucede y por lo tanto, también en poco tiempo llegarían a un punto de equilibrio. ¿Cuál es ese punto? ¿Quiere pensar usted?

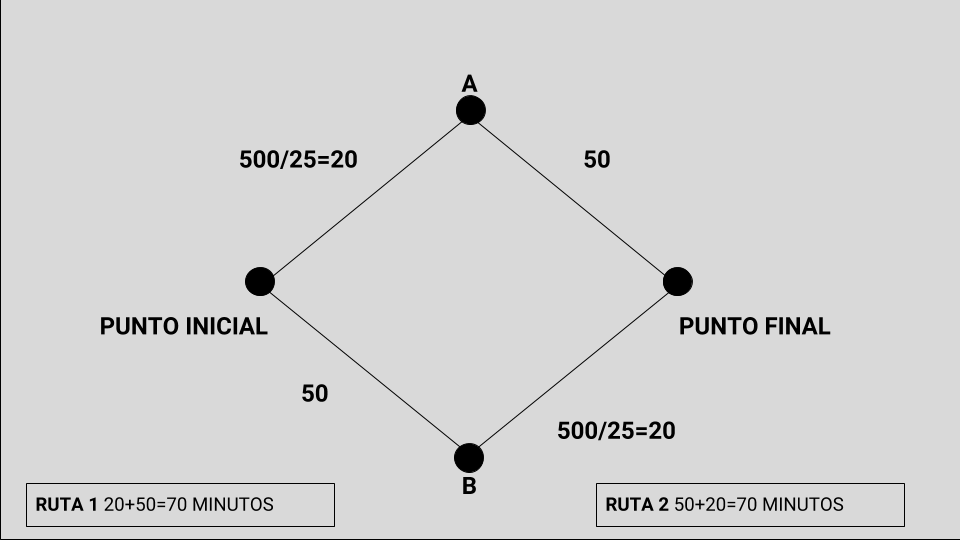
Efectivamente, en pocos días se llegaría a la situación en el número de autos (1000) se dividiría por mitades, y habría 500 que elegirían la ruta 1 y los otros 500, irían por la ruta 2 (Figura 7). Los vehículos tardarían 70 minutos por cualquiera de las dos rutas. Este es el punto de equilibrio.

Ruta 1:  500/25 + 50 = 20 + 50 = 70

Ruta 2:  50 + 500/25 = 50 + 20 = 70

 

 

Hasta acá está todo claro (creo). Sin embargo, ahora viene lo increíblemente curioso y anti-intuitivo. Supongamos que ahora uno construyó una ruta que uniera A con B (en ambas direcciones), es decir, un camino adicional que antes no existía. Eso le daría a los conductores la posibilidad de cambiar de la ruta 1 a la ruta 2 (y viceversa). Mire la Figura 8.

 

 

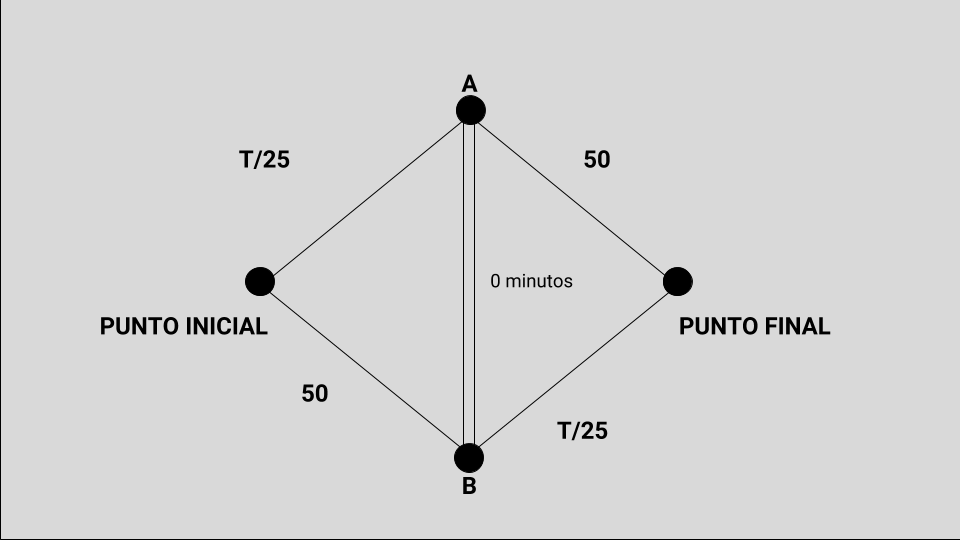
Para hacer las cuentas más sencillas, voy a suponer incluso que uno no tarda nada en recorrer ese camino. Es decir, le asigno CERO minutos a ir desde A hasta B o viceversa. ¿Qué pasará ahora? ¿Qué incidencia tendrá la aparición de este nuevo camino? Verá que lo que sucede es algo realmente fascinante… ¡e inesperado!

Antes de leer lo que yo escribí más abajo, haga usted algunas cuentas probando alternativas y anote los resultados que va obteniendo. Le estoy proponiendo que imagine potenciales rutas y les asigne un número determinado de vehículos que hayan optado por uno u otro segmento y tome decisiones sobre qué es lo que más convendría hacer en cada caso. Cuando usted haya analizado lo que usted considera como suficientes casos o conjeturas, ahora sí le propongo que nos embarquemos juntos en algunas ‘especulaciones’.

Sigo yo. Supongamos que usted se para en el punto Inicial y a diferencia de lo que sucedía antes, tendrá a su disposición el camino que une A con B. Supongamos que los mil vehículos decidieran ir por el segmento que une el punto inicial con A. En ese caso, resulta 1000/25 = 40 minutos.

Si ese mismo conductor se fija en lo que sucedería si elige el camino que une el punto inicial con B, descubriría inmediatamente que eso le insumiría seguro 50 minutos. Es decir, en el peor de los casos, en el que los mil vehículos elijan el camino que los lleva hasta A primero, aún así conviene elegirlo porque con ese trayecto uno tarda 10 minutos menos.

O sea: con el Ruta 1, aún con los 1000 vehículos yendo por la ruta que une el punto inicial con A, insumiría T/25 = 1000/25 = 40 minutos. Por otro lado, usando la Ruta 2, el que une el punto Inicial con B, seguro que uno tarda 50 minutos. No hace falta ser muy perspicaz para determinar que la mayoría (o todos) los conductores optarían por el camino 1.

Ahora bien: cuando llegue al punto A, ya tardó 40 minutos… ¡en el peor de los casos! Es decir, si todos los vehículos optaron por ese camino. Si algunos optaron por ir hasta B, eso, naturalmente reduciría el tiempo invertido, que como máximo entonces será de 40 minutos.

Cuando un conductor llegó hasta A habiendo tardado como máximo 40 minutos, ¿qué puede hacer? Tiene dos alternativas.

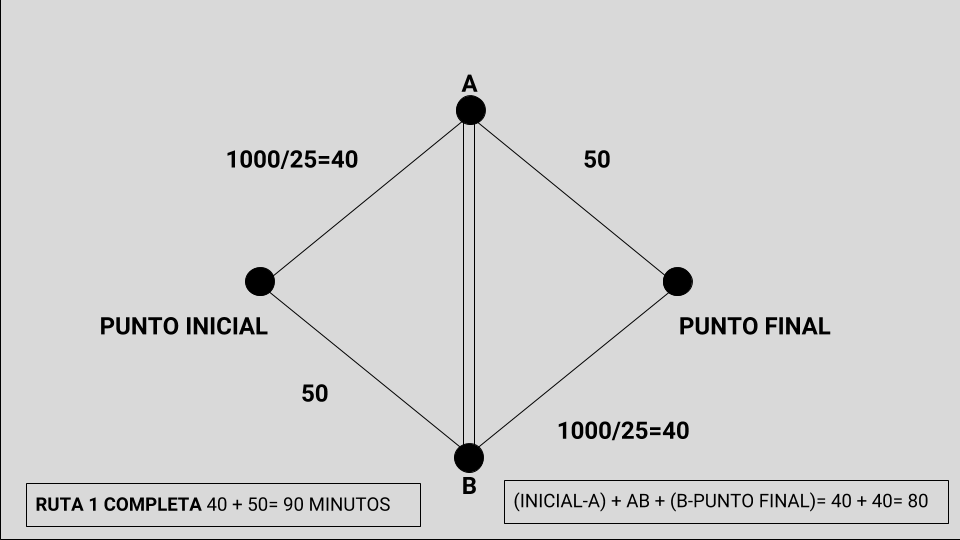
1- Si sigue por la Ruta 1 completa, tendrá que agregar a esos 40 minutos (como máximo), los 50 minutos que le faltan para llegar al punto Final. Luego, como 40 + 50 = 90, su tiempo usando completamente la ruta 1 le insumiría, en el peor de los casos, 90 minutos.

2- Si en cambio, usa la ‘nueva’ ruta, y viaja desde A hasta B (sin consumir ningún tiempo), y luego sigue desde B hasta el punto Final, tendrá que agregar a los 40 minutos, otros 1000/25 = 40 minutos más. Moraleja: al sumar los 40 para llegar a A, y luego cambiar a B y recorrer lo que le falta, tendrá que sumar 40 + 40, hasta llegar a 80 minutos.

Acá tengo una pregunta para hacerle: ¿qué conclusión saca usted? Si va por la Ruta 1 completa, tarda 90 minutos. Si en la mitad del camino va desde A hasta B, tarda 80 minutos.  Pero lo extraordinario es que cuando el camino desde A hasta B no existía, el tiempo que tardaba era de ¡¡¡¡70 minutos!!!! Es decir, en cualquiera de los dos casos, ¡tardaría más tiempo que lo que hubiera llevado si no existiera el camino intermedio!

 

 

¿Y entonces? ¿No estábamos tentados de pensar que al haber abierto un nuevo camino y una nueva alternativa, el tiempo se reduciría?

La paradoja de Braess intenta demostrar lo contrario. Cuando ese camino entre A y B no existía, los vehículos tardaban (en promedio) menos tiempo que aprovechando de la existencia de ese nuevo segmento.

Y esto es lo que quería compartir con usted ya que atenta fuertemente contra la intuición. Hay muchísima literatura escrita sobre el tema y aún hoy es ciertamente controversial, pero los números están allí y los ejemplos de las tres ciudades fueron nada más que disparadores. Usted tiene la palabra.

 

 

--------------------------------

Para suscribirte con $ 1000/mes al Cohete hace click aquí

Para suscribirte con $ 2500/mes al Cohete hace click aquí

Para suscribirte con $ 5000/mes al Cohete hace click aquí