Donde se descubre que la pizza puede ser útil para algo más que lo obvio
Cuando uno ve un mago, cuando lo ve operar, tiene varias alternativas: o bien trata de descifrar cómo hace lo que hace (y en general fracasa en el intento), o bien se deja engañar y acepta en forma racional que algún truco tiene que haber pero no invierte tiempo en tratar de descifrarlo. Estoy casi seguro de que se sienten más cómodas las personas que optan por la segunda alternativa, aunque más no sea porque uno se frustra menos. Pero lo que es indiscutible es que “la magia seduce”.
Acá me permito agregar: "La matemática también”.
El problema es que es una ciencia un poco (o un ‘mucho’) más invisible y no tan aparente. Pero hay muchos momentos en los que nuestro sentido común apunta para un lado y la realidad —ayudada por la matemática… para otro. Son los momentos en donde la intuición no funciona. De todas formas, como todo músculo, cuando uno lo entrena se hace cada vez más fuerte, más potente... y más útil también.
Quiero contar un ejemplo que siempre me fascinó. Contiene algunos elementos que no son usuales en nuestra vida cotidiana, pero estoy convencidísimo de que va a disfrutarlo y le permitirá agregar algunas herramientas (que a lo mejor ya tiene) a su arsenal intelectual. Ciertamente, no es poco.
Para graficar lo que quiero hacer voy a suponer que tenemos una pizza en forma de un cuadrado. Sí, ya sé: las pizzas no tienen esta forma habitualmente, pero concédame esa licencia. Ya verá que —al final— es algo de poca importancia.
Tengo entonces una pizza ‘cuadrada’ como se ve en la Figura 1. Como voy a tratar de alimentar a varias personas, supongamos que la pizza tiene un metro de lado. Es decir, tiene una superficie de ¡un metro cuadrado! Igualmente, como escribí más arriba, todos estos números terminarán siendo irrelevantes.
Eso sí: para fijar las ideas, todas las longitudes que aparezcan en este texto las voy a medir en metros y las superficies en metros cuadrados.
Sigo. Tomamos la pizza y la cortamos por la mitad primero y después, otra vez por la mitad en forma perpendicular, de manera tal que quede dividida en cuatro cuadrados iguales. La única diferencia es que ahora, cada una de las porciones cuadradas tiene medio metro de longitud. ¿Me siguió? Fíjese en la Figura 2.
Ahora calculemos el área. Como cada pequeño cuadrado tiene ½ metro de lado, la superficie de cada porción es de ½ x ½ = ¼ (metros cuadrados).
Una pausa: no me abandone ahora que todavía falta lo mejor. En definitiva, todo lo que hice hasta acá fue cortar una pizza y calcular la superficie de cada porción.
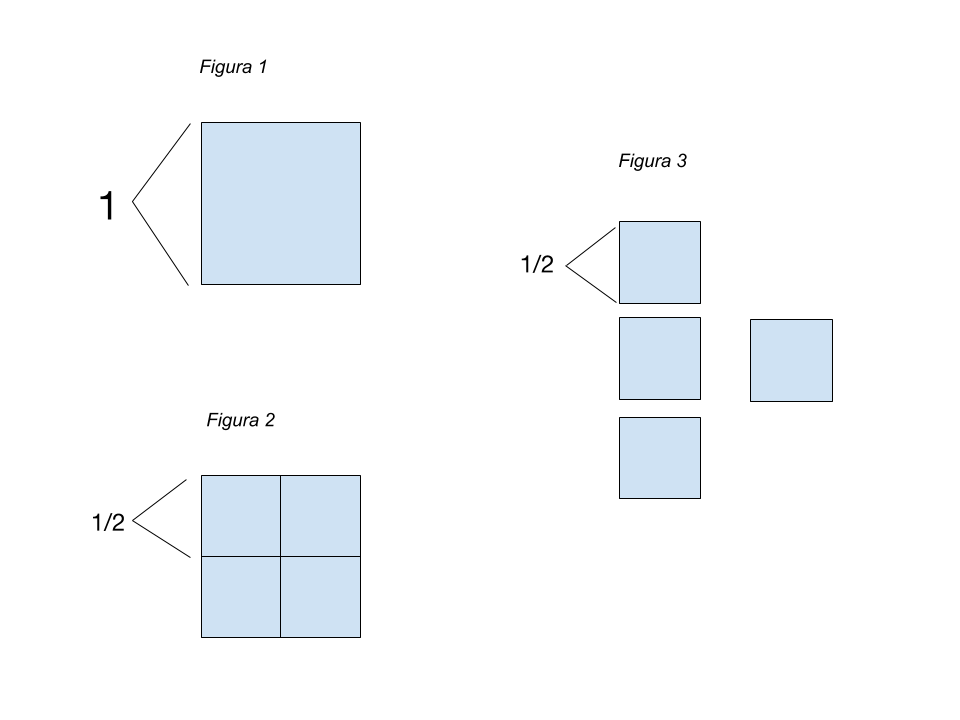
De los cuatro cuadraditos que se forman, separe tres y póngalos en una columna como en la Figura 3. Como se ve, el cuadradito restante lo puse a un costado.
Ahora, justamente con este cuadradito que sobró, hago lo mismo que hice recién con la pizza original, es decir, con el cuadrado grande. Lo vuelvo a dividir en cuatro cuadraditos iguales. Claro, como ahora la porción tiene ½ metros de lado, al cortarlas por la mitad cada lado del nuevo cuadradito medirá la mitad, o sea ¼, como se ve en la Figura 4.

Ya que está mirando la figura 4, fíjese que lo que hice fue tomar cada uno de esos cuadraditos de ¼ de lado y lo puse al lado de uno de los cuadrados originales (que tenían ½ de lado). Quedaron, como se ve, tres filas iguales. Cada una de ellas tiene uno de las porciones originales (la de un medio de lado), otra de lado un cuarto y todavía me queda un cuadradito sin cortar, que lo puse a un costado. Acépteme la sugerencia y revise las figuras que acompañan el texto para convencerse que estamos los dos hablando de lo mismo.
La idea ahora es replicar lo que hice antes y repetir la operación una y otra vez con los cuadraditos que van sobrando. Es decir: voy dividiendo cada uno de ellos como hice con la pizza original y de esta forma, voy consiguiendo cuadraditos cada vez más chicos, pero que tienen la particularidad que la longitud de cada lado es siempre la mitad del anterior.
Por otro lado, voy formando tres filas iguales. Cada una de ellas va teniendo un representante de cada una de las porciones que voy generando. La primera porción es un cuadrado que tiene medio metro de lado, la segunda mide la mitad, o sea ¼, la tercera la mitad de la anterior, o sea 1/8, después 1/16, 1/32... Así sucesivamente. Para convencerse, siga el ejemplo en las figuras 5 y 6.
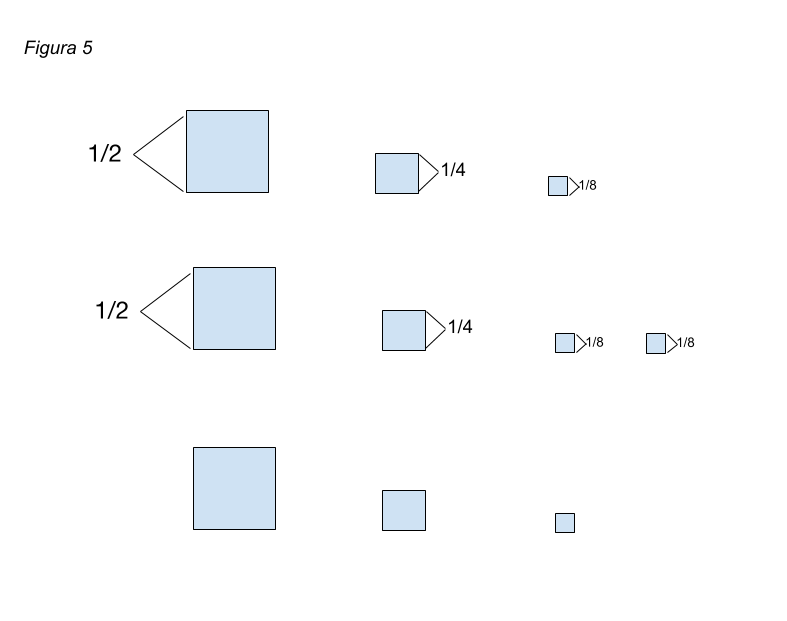
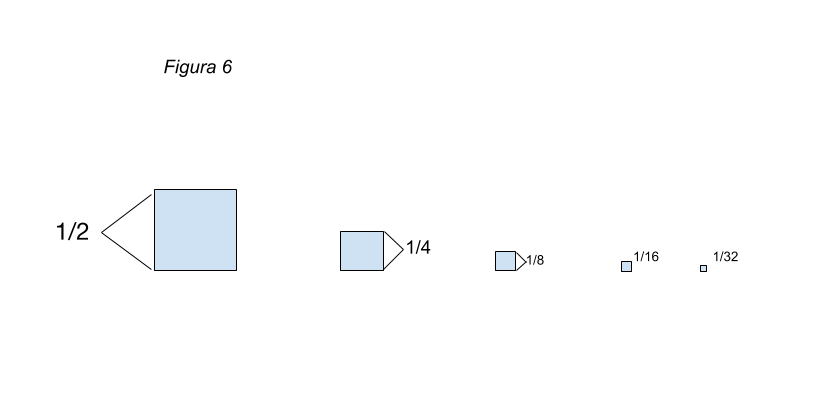
Ahora, acépteme la audacia de imaginarnos cortando la pizza ad infinitum... o sea en forma indefinida e ir construyendo las tres filas de la forma que expliqué más arriba.
Quiero hacer un par de observaciones:
- Es importante que usted se convenza que quedan formadas tres filas iguales. Cada fila contiene un representante (o porción) de las que fui consiguiendo al ir cortando la pizza en forma sucesiva. El primer cuadradito tiene ½ metro de lado, el segundo ¼, el tercero 1/8, el cuarto 1/16, el quinto 1/32, y así siguiendo infinitamente [1].
- Ahora concentrémonos en las áreas o superficies de los cuadraditos que aparecen en cada fila. Piense usted cómo hacer para calcularlas. El primer cuadradito tiene área ¼ (ya que cada lado mide ½). El segundo, tiene área 1/16, ya que este cuadrado tiene lado ¼. Si sigo en forma infinita, las áreas que aparecen van a ser: ¼, 1/16, 1/64, 1/256, 1/1024, 1/4096,..... O podríamos escribirlo así: (1/4), (1/4)2 , (1/4)3 , (1/4)4 , (1/4)5, (1/4)6, (1/4)7, ........ Como usted advierte, aparecen las potencias sucesivas del número (1/4).
No me abandone ahora porque estamos a punto de terminar.
Quiero hacerle la pregunta clave: ¿qué pasaría si yo sumara las áreas de todas las filas? ¿Cuánto dará?
Recuerde que la pizza original tenía una superficie de un metro cuadrado, ¿de acuerdo? Como lo único que hice fue cortar la pizza y distribuirla en tres filas iguales, la suma de todas las áreas tiene que seguir dando lo mismo, o sea, ¡tiene que seguir dando UNO!
Ahora, le propongo que calculemos el área de otra forma. Como las tres filas que construimos son iguales, las áreas también. Por lo tanto, como sabemos que la suma total de las áreas tiene que dar uno, cada una de las filas tiene que sumar la tercera parte, o sea 1/3. ¿Está de acuerdo conmigo? No avance si no me cree.
Sigo. Es que si uno tiene dividida una superficie en tres partes iguales, y la suma da uno, entonces, cada parte tiene que medir 1/3.
Ahora, el final a toda orquesta. Por un lado, sumemos las áreas de cada fila, teniendo en cuenta lo que sabemos que mide el área de cada cuadradito. Es decir:
(1/4) + (1/4)2 + (1/4)3 + (1/4)4 + (1/4)5 + (1/4)6 + (1/4)7 ....
Por otro lado, lo que sabemos también, es que la superficie de pizza que hay en cada fila es 1/3 de metro cuadrado.
Esta igualdad la puedo escribir así:
¼ + 1/16 + 1/64 + 1/256 + 1/1024.... = (1/4) + (1/4)2 + (1/4)3 + (1/4)4 + (1/4)5 + (1/4)6 + (1/4)7 .... = 1/3.
Lo quiero escribir de nuevo para enfatizarlo: hemos descubierto que –si uno acepta que puede sumar infinitamente—, la suma de las áreas de todos los cuadraditos que aparece en cada fila es exactamente igual a un tercio. Dicho de otra forma: si uno hace la suma de las potencias sucesivas del número (1/4), se obtiene... ¡1/3! ¿No es notable esto? [2]
Muchas veces las fórmulas impiden entender lo que está sucediendo por detrás, algo así como que el árbol tapa al bosque. Es por eso que el ejemplo de la pizza es muy útil no sólo para testear la intuición sino para imaginar lo que uno no ve. Y de paso, como suele suceder, cada vez que aparecen los infinitos involucrados, uno siente que entra en una suerte de dimensión desconocida, en donde todas las ‘verdades’ aparecen puestas en duda. ¿No es fascinante eso?
[1] Uno podría pensar que como voy cortando por la mitad la longitud de cada cuadrado, las porciones van teniendo como lados:(1/2), (1/2)2, (1/2)3, (1/2)4, (1/2)5, (1/2)6, (1/2)7, ... o sea, las potencias sucesivas del número (1/2).
[2] Este es un caso particular de algo mucho más general que tiene que ver con lo que se llama la ‘suma de una serie geométrica’. En cualquier libro de Cálculo Diferencial es posible encontrar (y demostrar) que la suma de una serie geométrica de ‘razón q’ es igual a (1/(1-q)). En el caso que nos ocupa, la razón es ¼. Para que el resultado tenga validez, el número q, tiene que ser, mayor que (-1) y menor que 1. Hay que omitir al primer término de la suma para que el resultado no sea 4/3, pero esas son cuestiones técnicas que en este contexto resultan irrelevantes.
--------------------------------Para suscribirte con $ 8.000/mes al Cohete hace click aquí
Para suscribirte con $ 10.000/mes al Cohete hace click aquí
Para suscribirte con $ 15.000/mes al Cohete hace click aquí

