Entre primos

 

Continuamos con los problemas irresueltos de las matemáticas que empezamos a difundir en la edición anterior.

 

2) La Conjetura de Goldbach

Christian Goldbach fue un matemático alemán pero también abogado. Corría el año 1742. La gran estrella de la matemática mundial era un matemático alemán también: Leonhard Euler. Goldbach le escribió una carta a Euler con la siguiente pregunta que él no podía contestar:

¿Es verdad que todo número par mayor que cuatro se puede escribir (o descomponer), como la suma de dos números primos?

Ejemplos:

1. 8 = 3 + 5. En este caso, 8 es el número par mayor que cuatro, y tanto 3 como 5 son números primos. ¿No tiene ganas de pensar usted? Fíjese que no dice que haya una única manera de descomponer al número par, sino que tiene que haber por lo menos una forma de hacerlo.
2. 10 = 5 + 5. Pero también se puede escribir 10 = 3 + 7.
3. 12 = 5 + 7.
4. 14 = 7 + 7 = 3 + 11
5. 16 = 5 + 11 = 3 + 13
6. 18 = 7 + 11 = 5 + 13
7. 20 = 7 + 13.
8. 22 = 11 + 11
9. 24 = 11 + 13.

Y así podría seguir. Hasta hoy, marzo del año 2018, se sabe que la conjetura de Goldbach es cierta para todo número par menor o igual que:

400.000.000.000.000.000

Es decir, uno tiene la fuerte tentación de decir que el resultado es cierto, que la conjetura de Goldbach se verifica, pero…. No alcanza con haber comprobado que es cierta para muchísimos números. Lo que hace falta es que alguien la demuestre para un número par cualquiera, y eso, ¡aún no se sabe!

 

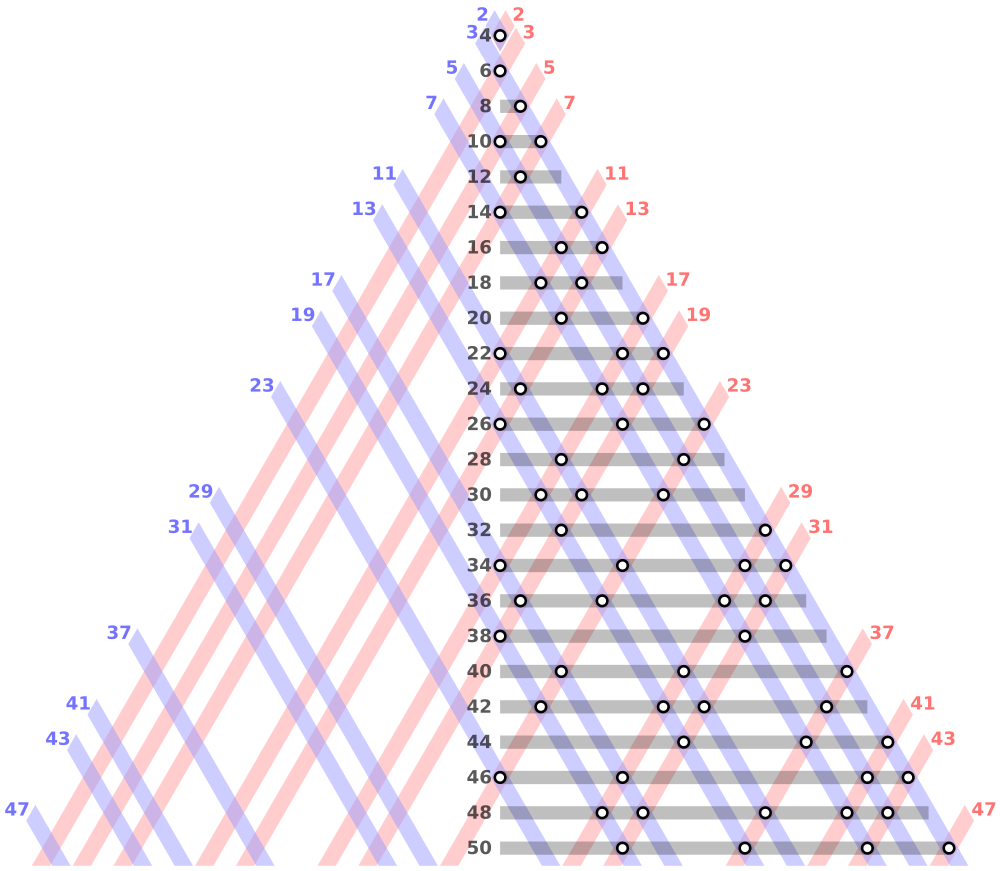
3) Primos Gemelos

¿Qué es un número primo? Para no hacer acá una larga exposición sobre los números primos en general, quiero hacer un breve resumen (para lo que importa en este contexto): un número entero positivo mayor que uno se dice primo si tiene nada más que dos divisores: él mismo y el número 1.

Por ejemplo, el número 2 es un número primo, porque tiene EXACTAMENTE dos divisores (positivos): 1 y 2. Por la misma razón, el número 3 es primo (divisible por 3 y por 1). A partir de acá voy a omitir al número 1, porque está claro que 1 divide a todo número. Ahora bien: el número 4, por ejemplo, no es primo, porque no solo es divisible por él mismo, sino que también es divisible por 2. El 7 es primo pero el 15 no (15 es divisible por 3 y por 5).

La lista de los primeros números primos empieza así:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, ….

Uno podría preguntarse: ¿hay infinitos primos?

Al mismo tiempo, y esto es muy curioso, la respuesta se conoce desde más de dos mil años (sí, más de 2.000 años), porque Euclides probó (en forma realmente sencilla) que sí, que efectivamente hay infinitos números primos. No lo voy a demostrar acá, pero si le interesa el tema, en casi cualquier texto de aritmética universitaria, es posible encontrar la prueba en los primeros capítulos.

Hay muchísimas preguntas no contestadas cuando uno habla de números primos, pero la que quiero presentar tiene un costado atractivo extra por su parte. Sígame y verá qué interesante.

Si usted piensa un instante, se dará cuenta que hay un solo número primo positivo par.  Me refiero al número 2. Pero a partir de allí, cualquier otro número par mayor que dos, no puede ser primo, porque esencialmente, ¡será divisible por 2! (además de por sí mismo y por 1).

Dicho esto entonces, piense conmigo lo siguiente: exceptuando el caso muy particular del 2 y 3… ¡no puede haber números primos consecutivos! ¿Por qué? Es que si usted elige dos números seguidos (o consecutivos), uno de los dos tiene que ser par, y por lo tanto, uno de los dos (o los dos) no pueden ser primos. Ahora tomemos por ejemplo dos números primos no consecutivos, pero ‘casi’. ¿Qué quiero decir con ‘casi’? Quiero decir que me voy a permitir saltearme un número que esté entre los dos.

Por ejemplo, tomemos al 3 y al 5. Los dos son primos (en este caso, me salteé el 4). Podría hacer lo mismo con 5 y 7 (salteando el 6). O el 11 y el 13 (salteando el 12). Si quiere, podríamos irnos un poco más ‘adelante’ entre los números enteros positivos. Por ejemplo, (17,19), o (29, 31), o bien (59,61)… o (71,73). A cada par de primos que cumplen esta característica (ser dos números primos ‘casi consecutivos’, salteando al número par que está en el ‘medio’), se los llama “primos gemelos”.

Al llegar acá entonces, pregunta: ¿hay infinitos pares de primos gemelos?

Es decir, como escribí más arriba, uno sabe que hay infinitos primos (lo probó Euclides), pero lo que no sabe es que haya infinitos primos gemelos… ¡Y esa es el problema irresuelto que quería contar acá! [1].

 

 

 

 

[1] Cuando Carlos D’Andrea llegó a este punto en la revisión que hace de los textos que le envío, me escribió un mail: “Adrián, hay un cierto ‘progreso’ reciente respecto del problema, pero el progreso ha llegado de una manera muy interesante. Lo que se consiguió demostrar es que hay infinitos pares de primos que difieren en un número fijo N (el caso particular de la conjetura es cuando N = 2), pero en un comienzo el número N estaba alrededor de los 70 millones. Hoy, mientras te escribo esto, el N ya se redujo a… ¡seis! Los matemáticos que más han aportado son Yitang Zhang (que publicó su trabajo en el Annals of Mathematics en mayo del 2013), y también James Maynard y Terence Tao (¡cuando no! ‘Este comentario me pertenece’).

 

 

 

 

--------------------------------

Para suscribirte con $ 1000/mes al Cohete hace click aquí

Para suscribirte con $ 2500/mes al Cohete hace click aquí

Para suscribirte con $ 5000/mes al Cohete hace click aquí