Mohan Srivastava es un matemático canadiense, cuya especialización es programación y análisis estadístico. Hace 15 años, en junio del 2003, Mohan encontró en su casa en Toronto [1], unos billetes ‘viejos’ de lotería, una de las múltiples variantes que hay en todo el mundo. En este caso, era el equivalente de nuestra ‘raspadita’. (¿Se sigue llamando así?) Curiosamente, los billetes tenían los números cubiertos; es decir, todavía ningún miembro de su familia había intentado ‘rasparlos’ para ver si eran ganadores o no. Juegos de estas características abundan en distintos lugares del mundo, no solo en la Argentina, pero la variante de la que quiero hablar involucra ni más ni menos que… el ta-te-ti.Tengo ganas de asumir que usted sabe cómo se juega, pero escribo acá una versión abreviada de las reglas. ¿Cómo se juega al ta-te-ti? En un tablero de 3×3, compiten dos personas. Digamos que una juega con letras ‘x’ y otra con letras ‘o’. Alguno de los dos empieza (y esa es una ventaja muy clara en el juego), y después se alternan. El objetivo es poner tres iguales en alguna fila o columna o en alguna de las dos diagonales. Es un tradicional juego con una estrategia muy sencilla en donde uno, si juega correctamente, puede que no gane, pero seguro que no pierde.
En un tablero de 3×3, compiten dos personas. Digamos que una juega con letras ‘x’ y otra con letras ‘o’. Alguno de los dos empieza (y esa es una ventaja muy clara en el juego), y después se alternan. El objetivo es poner tres iguales en alguna fila o columna o en alguna de las dos diagonales. Es un tradicional juego con una estrategia muy sencilla en donde uno, si juega correctamente, puede que no gane, pero seguro que no pierde. 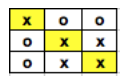 Ahora quiero contar la variante canadiense de nuestra ‘raspadita’ con la participación estelar del ta-te-ti. En cada billete, había dos partes claramente separadas. La que dice ‘Sus números’ (que está a la izquierda) consiste en dos columnas de 12 cuadraditos cada una. Cada uno de estos cuadraditos tiene un número que no se ve, porque está tapado por una ‘o’ o una ‘x’. Esos serán los casilleros que uno deberá raspar para saber si ganó (o no).Por otro lado, en el costado derecho del billete, como se ve en la Figura 1, hay ocho ‘tableros’ de ‘ta-te-ti’.Cada uno de ellos tiene nueve cuadraditos y cada uno de esos cuadraditos contiene un número elegido entre 1 y 39.
Ahora quiero contar la variante canadiense de nuestra ‘raspadita’ con la participación estelar del ta-te-ti. En cada billete, había dos partes claramente separadas. La que dice ‘Sus números’ (que está a la izquierda) consiste en dos columnas de 12 cuadraditos cada una. Cada uno de estos cuadraditos tiene un número que no se ve, porque está tapado por una ‘o’ o una ‘x’. Esos serán los casilleros que uno deberá raspar para saber si ganó (o no).Por otro lado, en el costado derecho del billete, como se ve en la Figura 1, hay ocho ‘tableros’ de ‘ta-te-ti’.Cada uno de ellos tiene nueve cuadraditos y cada uno de esos cuadraditos contiene un número elegido entre 1 y 39.
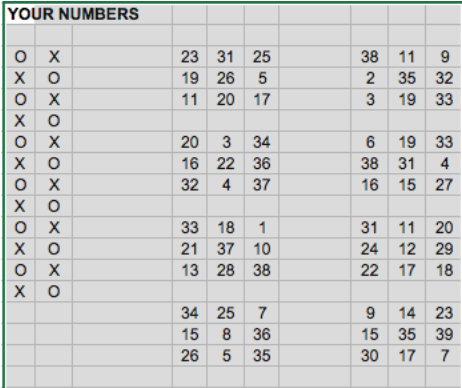
Figura 1
Hasta acá, es lo que uno ve cuando compra un billete. ¿Cómo hacer para ganar? Tiene que pasar lo siguiente. Usted empieza por raspar los 24 números que tiene a la izquierda. Ahora queda un ‘dibujo’ como el que se ve en la figura que está acá abajo:
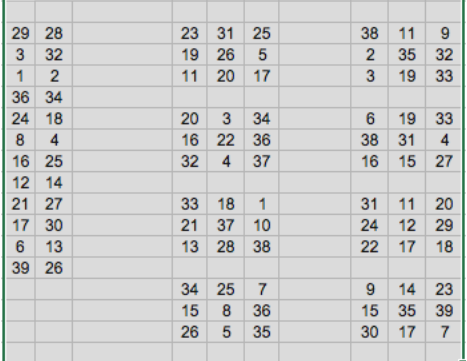
Figura 2
Ahora concentre su atención en los ocho tableros que están a la derecha. Tomemos el primero de ellos, el que está más arriba y a la izquierda. Por ejemplo: la segunda fila está formada por el 19, 26 y 5. Entonces, usted se fija en los 24 números que recién ‘raspó’ y trata de encontrarlos. El 19 no está, y eso es suficiente para buscar en otro lado. De esa forma, en cada tablero, usted va reproduciendo lo que hice recién con la segunda fila del primer tablero. Si usted encuentra alguna terna entre los números que tiene a la izquierda, de manera tal que los tres estén en una fila o una columna o alguna de las dos diagonales de alguno de los tableros… eso significa que ese billete… ¡es GANADOR! Mire esta figura:
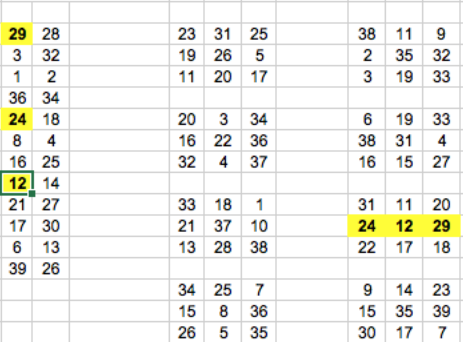
Figura 3
En este caso, usted tiene (entre sus números), el 29, el 24 y el 12 (que yo marqué a la izquierda). Ahora, mire los tableros que están a la derecha. El sexto, tiene justamente, los números 24, 12 y 29 que forman una fila ‘ganadora’ para el ta-te-ti. Como escribí más arriba, esto le alcanza para ganar.Pero, si usted mira la fila de abajo (22, 17 y 18), esa es perdedora porque si bien usted tiene el número 17 y también el 18, le falta el 22.Creo que ahora está claro cómo es el juego, que como usted advierte, es muy sencillo.Vuelvo a la historia. Srivastava descubrió que entre los billetes ‘viejos’ que había encontrado, uno era ‘ganador’. Era muy poco dinero (solamente tres dólares canadienses), pero de todas formas… ¿por qué regalar dinero, no es así? Se fijó en todos los otros, y ese era el único con premio.Mientras iba a cobrar lo que le correspondía, a Srivastava, que obviamente tiene una mente preparada o entrenada para pensar, se le ocurrió algo muy racional (y le pido que me acompañe en este tramo, que es uno de los más importantes de todo este texto).“Estos billetes no se hacen a mano; tiene que haber algún programa de computadora que los prepara. Tiene que haber algún algoritmo escrito por algún humano que esté detrás de todo esto. Este algoritmo es el que produce algunos billetes ganadores y otros… la enorme mayoría… tienen que ser perdedores”.La pregunta entonces era: ¿Podría ser que los números que aparecieran a la izquierda fueran elegidos al azar? Por un lado, él sabía bien que eso no podía ser cierto. La lotería no puede correr el riesgo de que haya muchísimos billetes ganadores. Seguro que tiene un presupuesto que distribuirá entre los que acierten y por eso, ¡alguien tenía que controlar cuántos billetes ganadores habrían de imprimir! Y para hacer eso, algún humano tiene/tenía que tener ese particular control.¿Qué diría el algoritmo? ¿En qué consistía? ¿Habría acaso algún patrón que él pudiera descubrir de manera tal que, sin tener que raspar, se pudiese distinguir los billetes que terminarían siendo ganadores?A esta altura es posible que cualquiera de nosotros (usted que está leyendo y yo que estoy escribiendo), haya tomado la decisión de abandonar, porque es muy probable que a cada uno de nosotros nos resulte poco creíble que la lotería pueda cometer un error tan sencillo. Los billetes no pueden ser tan vulnerables, tal que una persona solo ‘imaginando’ que tiene o tendría que haber un error, lo pueda encontrar tan fácilmente. ¿En dónde habría de estar el patrón que buscaba Srivastava? ¿Lo podría llegar a descubrir? El estaba convencidísimo (y lo bien que hacía) en saber que tenía que haber UN PATRON… en alguna parte tenía que estar… todo bien, pero ¿cuál era? Y … ¿dónde estaba?Curiosamente, después de pensar por un día, tuvo una idea. Se le ocurrió una posibilidad que estuvo a punto de desechar porque le pareció muy fácil. Pero, fácil o no, ya no se habría de entregar. La única manera que tenía de comprobar si su teoría era verdadera, era ir y comprar algunos billetes que “él creía que tenían que ser ganadores… ¡y ganar!” Aunque fuera poco dinero, eso era irrelevante: lo importante era confrontar su teoría con la realidad.Acá es donde quiero escribir sobre lo que pensó (y descubrió) y verá que es una idea muy sencilla. Bueno, es sencilla una vez que uno sabe que es cierta y además, una vez que se le ocurrió ‘a otro’. Más aún: ¡hasta parece mentira! Sígame por acá.Vuelva conmigo a mirar un billete. A la derecha están los ocho tableros de ta-te-ti. Cada tablero tiene nueve casilleros. En total, como 8 x 9 = 72, eso significa que en total, hay 72 casillas para rellenar con números. Hasta acá, todo bien. Pero como escribí al principio, los números que aparecen en los casilleros tienen que estar elegidos entre 1 y 39. Luego, inexorablemente ¡tiene que haber repeticiones! ¡Y varias repeticiones! Los números no pueden ser siempre distintos, porque no hay suficientes números para que eso suceda. Podría ser también que algunos números no figuraran directamente, pero también podría ser que algún número apareciera cuatro veces… o cinco. Pero acá aparece la esencia de la idea. Lo que Srivastava pensó fue lo siguiente: ¿habrá algunos números que aparezcan una sola vez? Y si hubiera números que aparecen una sola vez, ¿formarán acaso alguna fila o columna o diagonal de alguno de los tableros?Al llegar acá, Srivastava estaba por explotar. NECESITABA conseguir billetes y su intención de ir al kiosko estuvo basado mucho más en la necesidad de comprobar su conjetura que cobrar los tres dólares que había ganado en otro momento.Y fíjese lo que hizo. Vaya ahora a la Figura 3. El primer número que aparece en el primer tablero es el número 23. ¿Cuántas veces aparece el número 23 sumando todos los tableros? Contemos (y le propongo que lo haga usted también, para convencerse que está siguiendo lo que escribo). El número 23 aparece en el primer tablero, en la primera columna, primera fila, y aparece también en el último tablero de la derecha, si usted se fija en la primera fila pero en la tercera columna, allí aparece también el número 23. ¡Y no está en ningún otro tablero, en ningún otro lugar! O sea, en total, el número 23 aparece dos veces.Sigamos analizando algunos otros ejemplos.
- Tome el 31, que está también en el primer tablero, primera fila pero ahora segunda columna. Ayúdeme a buscar si aparece otra vez. Lo encontré en el cuarto tablero, a la derecha, en la segunda fila, segunda columna. Y aparece una tercera vez, en el sexto tablero (estoy contando de arriba hacia abajo y de izquierda a derecha), esta vez en la primera fila, primera columna. Y no aparece más. O sea, el 31 aparece tres veces.
- Busquemos lo que sucede ahora con el número 2. Si usted se fija por su cuenta, verá que solamente aparece en el segundo tablero, en la segunda fila y primera columna. Y nada más. Es decir, el número 2, ¡aparece una sola vez!
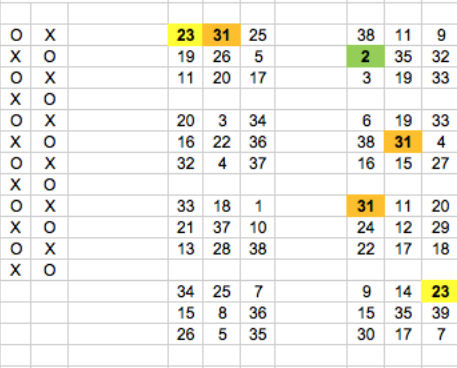
Figura 4
Como usted ve, Srivastava estaba interesado únicamente en los números que figuraban una sola vez entre todos lo tableros. ¿Cómo completó la idea?Si usted mira la Figura 4, verá que Srivastava fue ubicando en cada tablero, el número de veces que aparece cada uno de los números que corresponden a ese lugar en el tablero. Por ejemplo, el número 23 aparece dos veces, y por eso hay un número 2 en el primer tablero de arriba a la izquierda, en la primera fila y primera columna. Por otro lado, aparece un 3 en el mismo tablero, otra vez en la primera fila pero ahora en la segunda columna, y eso sucede porque como vimos más arriba, el número 31 aparece 3 veces. De la misma forma, si usted se fija en el segundo tablero, en la segunda fila y primera columna, aparece un número 1. ¿Por qué? Porque el número 2, está solamente en un solo tablero y aparece una sola vez.Con todos los datos que escribí hasta acá, le pido que usted complete lo que sucede con todos los números. Debería quedarle la Figura 4.
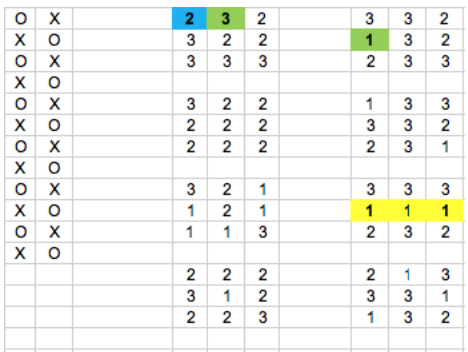
Figura 5
Ahora, vaya hasta la Figura 6:
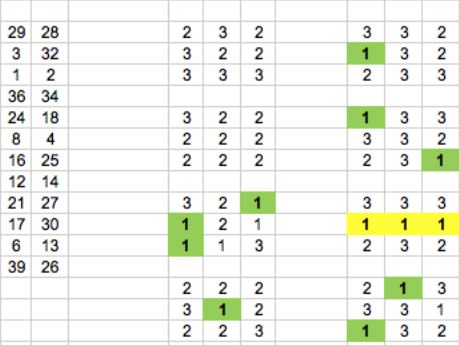
Figura 6
En este caso se ve claramente que hay tres números 1, que están formando una fila completa del tablero número seis. Bastará fijarse cuáles son esos números en la Figura 1. Esos números son 24, 12 y 29, que como usted ve, están entre los 24 números que él raspó. Srivastava raspó y encontró lo que sospechaba: ¡era un billete ganador!Por otro lado, comenzó a hacer las cuentas para determinar cuánto tiempo le llevaría distinguir cuáles serían ganadores y cuáles no. El dinero que podría ganar por hora, no le compensaba sacrificar su trabajo, en donde su salario superaba largamente lo que obtendría ganándole a la lotería jugando a esta versión paga de ‘ta-te-ti’.Sin embargo, decidió hacer algo de absoluta generosidad: ¡avisarle a las autoridades sobre lo que pasaba!Lo hizo, entregándoles un sobre y detallando lo que sucedía, pero después de esperar una respuesta, determinó que a nadie le interesaría ni siquiera leer una carta de ese tipo. Supuso que habría muchísima gente que debía creer que había descubierto algún artilugio para ganar. La Lotería de Ontario debía descartarlas a todas.Pero Srivastava no se quería dar por vencido. ¿Sabe qué hizo? Compró 20 billetes, pero no ‘raspó’ ninguno. Los eligió de manera tal que 10 fueran ‘perdedores’ y 10 fueran ‘ganadores’. Los metió en dos sobres distintos y los dejó en persona en la sucursal central de la Lotería de Ontario, a las 10 de la mañana. Dos horas después, recibió una llamada de la máxima autoridad indicándole que Srivastava había predicho 19 de los 20 billetes y que a partir del día siguiente, retirarían de circulación todos los billetes de ta-te-tí de TODA CANADA.La historia continúa, porque con toda razón, Srivastava sospechó que todas las ‘raspaditas’ o billetes que involucraran este tipo de ‘diseño’, tenían que tener algún tipo de patrón. Si él había podido con uno, ¿por qué no probar con otros? Por otro lado, ¿podría creerse él que justo había encontrado de todas posibles variantes la ÚNICA que se podía violar?Le pidió a un amigo en Colorado que le comprara billetes de lotería que involucraran ‘raspaditas’. Y tal como sospechaba, ¡el mismo truco permitía descubrir los billetes ganadores! Ahora no era tan seguro como en Canadá, porque solamente el 70 por ciento (de los que él probó), tenían premio, pero aún así….Aunque parezca mentira, todavía se producen este tipo de ‘descubrimientos’ . Srivastava no está solo, y hay mucha gente que sigue aprovechando del conocimiento que tiene o la capacidad para descubrir el algoritmo que está ‘detrás de lo que se ve’, y hay mucha gente que usa este tipo de recursos, incluso, para lavar dinero.Continuará… (O mejor dicho: continuaré.) [1] El artículo original y quien debería quedar con todo el crédito, apareció en la revista Wired, el 31 de enero del año 2011. Lo escribió Jonah Lehrer y se puede encontrar en su versión inglesa (original) acá: https://www.wired.com/2011/01/ff-lottery/ Otro texto que me sirvió, fue el que apareció en el diario “The Star”, el principal diario de Toronto. Se puede encontrar acá: https://www.thestar.com/news/
Para suscribirte con $ 8.000/mes al Cohete hace click aquí
Para suscribirte con $ 10.000/mes al Cohete hace click aquí
Para suscribirte con $ 15.000/mes al Cohete hace click aquí

